Запуск PRADIOS

PRADIOS может быть запущен с использованием различных методов, описанных здесь.

Из команднной консоли

команднная консоль — это самый простой способ запустить вычисления PRADIOS.

Он включает в себя интерактивный графический интерфейс для выбора входных файлов, определения параметров запуска, отправки нескольких запусков решателя с использованием очереди, планирования задержки, остановки задания, а также содержит все предопределенные переменные среды, необходимые для запуска PRADIOS.

В Windows команднную консоль можно запустить с помощью Пуск > 2022 > команднная консоль.

команднную консоль можно запустить из программного обеспечения, выбрав Справка > Руководство по команднной консоли.

На всех платформах эту утилиту можно запустить из командной строки.

Linux

<install_dir>/Laduga/scripts/PRADIOS -gui

Windows

<install_dir>/hwsolvers/scripts/PRADIOS.bat -gui

Ввод имя файла

На основании имени файла команднная консоль автоматически определяет, следует ли запускать Engine или Starter.

По умолчанию будут запущены все файлы Starter и Engine в каталоге файла. Можно легко запустить несколько файлов, поместив их в тот же каталог, что и стартовый файл.
Если выбран файл Engine, то он будет запущен, а затем все остальные файлы Engine в каталоге.
Если используется опция -onestep, будет запущен только выбранный входной файл. Запускается только файл Starter, если входной файл является файлом Starter, и запускается только файл Engine, если входной файл является файлом Engine.

Часто используемые параметры запуска

Вариант

Аргумент

Описание

-onestep

Н/Д

Отключить автоматическое продолжение к следующему Engine, запуск только Starter для

одиночного формат файла.

-nt

Количество потоков

Количество потоков SMP на домен SPMD MPI (Пример: PRADIOS ROOTname_0000.rad –nt 2)

-np

Количество доменов SPMD MPI

Количество доменов PRADIOS SPMD MPI. (Пример: PRADIOS ROOTname_0000.rad –np 12)

Все доступные варианты запуска

Любые аргументы, содержащие пробелы или специальные символы, должны быть заключены в кавычки {}, например

-mpipath {C:/Program Files/MPI}

Пути к файлам в Windows могут использовать обратную косую черту «» или косую черту «/», но при использовании обратной косой черты «» они должны быть заключены в кавычки.

Вариант	Аргумент	Описание	Доступные платформы
`-altver`		Суффикс для альтернативной версии программы решения.	Все платформы
`-appfile`	N/A	Файл спецификации с некоторым MPI для запуска SPMD.	Все платформы
`-args`		Дополнительные аргументы, передаваемые в решающую программу. Пример: `\\"\\{-x\\} \\{-f=C:/имя файла/ путь\\}\\"`	Все платформы
`-check`		Проверьте модель на наличие предупреждений и ошибок. Отключит декомпозицию домена и перезапустит запись файла.	Все платформы
`-checkpoint`	N/A	Запустите PRADIOS Engine, начиная с файла сохранения контрольной точки.	Все платформы
`-debug`	1, 2	Вывод информации об отладке сценариев.	Все платформы
`-delay`	Количество секунд	Задерживает запуск PRADIOS на указанное количество секунд. Эта функция не использует лицензии, память компьютера или процессор. до начала пробега (срок задержки истекает). Эту опцию можно использовать для ожидания любых вычислительных ресурсов. которые в настоящее время можно использовать, но еще не освобождены при предыдущем запуске. Если предыдущий запуск завершился сбоем, лицензия все еще может быть блокируется сервером значение тайм-аута, иначе память все еще может быть зарезервирована операционной системой. Примечание: 1. Опция `-delay` применяется к текущему заданию. Если работа отправлена на очередь командной консоли, то задержка начнется после Командной консоли разрешающей выполнение этого задания. 2. Если запуск производится с помощью Командной консоли, следует использовать параметр «Задержка по расписанию», чтобы отложить запуск очереди.	Все платформы
`-dylib`	ФАЙЛ	Задайте имя динамической библиотеке для пользовательских подпрограмм PRADIOS.	Все платформы
`-hostfile`	ТЕКСТ ФАЙЛ	Текстовый файл, в котором перечислены хосты и количество ядер для запуска нескольких компьютеров (узлов). Точный формат см. в документе MPI.	Все платформы
`-HSTP_READ`	NA	Прочтите файл `hst_input.hstp` и замените /PARAMETER входной колоды на те, которые определены в прочитанном файле.	Все платформы
`-HSTP_WRITE`	NA	Напишите файл <root_name>_0000.rad2hst `` , содержащий информацию о модели ``/PARAMETER.	Все платформы
`-mpi`	i , pl, ms	Укажите, какое программное обеспечение MPI используется для многопроцессорного запуска. `i` Intel MPI `pl` IBM Платформа-MPI (ранее HP-MPI) `ms` Microsoft MPI Примечание: Аргумент для `-mpi` не является обязательным. Если аргумент не указан, по умолчанию используется Inte MPI.	Не все платформы поддержка всего программного поддержка всего обеспечения MPI.
`-mpipath`	ДИРЕКТОРИЯ	Укажите путь, по которому находится mpirun. (Моделирование включает программное обеспечение MPI, поэтому обычно оно не требуется).	Все платформы
`-noh3d`	N/A	Не создавайте файл h3d из файлов анимации PRADIOS после завершения симуляции.	Все платформы
`-norst`	N/A	Удалите все файлы перезапуска (*.rst) после завершения моделирования.	Все платформы
`-np` or - `-nspmd`	Количество доменов SPMD MPI	Количество доменов PRADIOS SPMD MPI. Пример: `PRADIOS -np 4 ROOTname_0000.rad`	Все платформы
`-nt` or - `-nthread`	Количество ниток	Количество потоков SMP на домен SPMD MPI. Пример: `PRADIOS -i ROOTname_0000.rad -np 4 -nt 2`	Все платформы
`-nt_r2r`		Количество потоков процессора для многодоменного процесса.	Все платформы
`-onestep`	N/A	Отключите автоматическое продолжение к следующему файлу движка или мода, запускайте только Starter для одного формата файла	Все платформы
`-outfile`	ДИРЕКТОРИЯ	Определяет каталог выходных файлов для всех файлов, созданных Starter и Engine.	Все платформы
`-radfiles`	N/A	Перечислите все файлы в текущей папке с обнаруженными типами (Starter/Engine/mod).	Все платформы
`-radopt`	.radopt- файл	Возможность запуска оптимизации PRADIOS с помощью OptiStruct. Он указывает на запрос оптимизации для входной колоды PRADIOS. Примечание: Стартер PRADIOS и входные файлы, поддерживающие ввод оптимизации, должны быть доступны в том же каталоге, что и файл `<name>.radopt`. Дополнительную информацию см. в разделе «Оптимизация дизайна».	Все платформы
`-rseed`	источник	Необязательное значение: установите начальное значение для узлового случайного шум (0≤начальное значение<1).	Все платформы
`-rxalea`	xalea	Активация узлового случайного шума c значением xalea (xale a≥0).	Все платформы
`-sp`	N/A	Укажите запуск версии PRADIOS с одинарной точностью.	Все платформы
`-v`		Требуемая версия программы если установлено несколько Если не указано, используется последняя установленная версия. Пример: `PRADIOS -v 14. 0.220 ROOTname_0000.rad`	Все платформы

Решения управление

Если на начальном экране ввода командной консоли установлен флажок Использовать управление выбором, при запуске анализа появится окно просмотра. Это позволит пользователю выбрать один из вариантов (INFO, STOP, KILL, H3D, ANIM, RFILE и CHKP) и нажать Отправить команду. Более подробную информацию обо всех этих параметрах см. в разделе «Управляющий файл (C-файл)».

Рисунок 1:

Примечание: Опцию ANIM или H3D можно использовать для создания дополнительного файла анимации в текущее или указанное время или цикл. Это очень полезно, если вы хотите увидеть состояние симуляции. Опция STOP может остановить анализ и создать файл перезапуска, который позже можно будет использовать для продолжения решения.

Из сценария моделирования

Запустите PRADIOS из командной строки, используя сценарий, включенный в HyperWorks.

Этот сценарий следует использовать при запуске PRADIOS в кластере высокопроизводительных вычислений через планировщик заданий, поскольку многие переменные среды уже определены, что упрощает настройку. Все параметры, доступные в командной консоли, можно использовать из командной строки.

Для запуска в Linux из командной строки введите следующее:

<install_dir>/Laduga/scripts/PRADIOS «filename» -option argument

Для запуска из командной строки Windows DOS введите следующее:

<install_dir>\\hwsolvers\\scripts\\PRADIOS.bat "filename" -option argument

Параметры сценария описаны в разделе «Все доступные параметры запуска».

Из HyperMesh

При создании конечно-элементной модели PRADIOS в HyperMesh симуляцию можно запустить непосредственно в HyperMesh, перейдя на панель PRADIOS.

Доступ к панелям можно получить через страницу «Анализ», через меню «Утилиты» или через меню «Приложения». Панель запросит имя входного файла. После нажатия кнопки Экспорт модель экспортируется с использованием заданных параметров экспорта. Затем решатель запускает сценарий, который имеется локально на компьютере. После выполнения Solver результаты можно просмотреть в HyperView, нажав HyperView.

Примечание: В Linux при запуске PRADIOS из HyperMesh создается оболочка с Настройка ДИСПЛЕЯ <имя хоста>:0.0. Если это значение отличается от настройки ДИСПЛЕЯ для HyperMesh, 25/38 блоков Laduga (в дополнение к 21 блоку Laduga, используемому для HyperMesh) будут проверены. Чтобы избежать извлечения дополнительных модулей, перед запуском HyperMesh убедитесь, что для DISPLAY установлено значение <имя хоста>:0.0. до запуска HyperMesh.

Запуск исполняемого файла напрямую

Исполняемые файлы PRADIOS можно запускать напрямую, но необходимо определить различные переменные среды.

Поэтому рекомендуется и проще использовать сценарий PRADIOS, включенный в базовое моделирование, при запуске заданий на компьютерном сервере. Если по-прежнему необходимо запускать исполняемые файлы напрямую, необходимо установить следующие переменные среды:

RADFLEX_PATH = <install_dir>/hwsolvers/common/bin/<platform>/

RAD_H3D_PATH = <install_dir>/hwsolvers/PRADIOS/lib/<platform>/

HWSOLVERS_TEMPLEX =<install_dir>/hwsolvers/common/bin/<platform>/

ABF_PATH = <install_dir>/hwsolvers/PRADIOS/bin/<platform>/

RAD_CFG_PATH = <install_dir>/hwsolvers/PRADIOS/cfg/

При использовании версии SMP также следует определить переменную среды размера стека для каждого потока.

Linux KMP_STACKSIZE =400m

Windows KMP_STACKSIZE =400m

Только Windows

Обновите переменную среды PATH=%PATH%;\<install_dir>\hwsolvers\common\bin\win64;\<install_dir>\hwsolvers\PRADIOS\lib\win64

Только Linux

LD_LIBRARY_PATH=<install_dir>/hwsolvers/common/bin/linux64/:<install_dir>/ hwsolvers/PRADIOS/lib/linux64

Размер стека должен быть установлен на неограниченный размер с помощью этих команд в зависимости от оболочки входа.

Использование оболочки csh
ограничить размер стека неограниченно

Используя sh-оболочку
безлим -s неограниченно

Исполняемые файлы PRADIOS можно найти в <install_dir>\hwsolvers\PRADIOS\bin\<platform>\.

Теперь запустим Starter и Engine PRADIOS:

./s_<version>_<platform> –i <arguments> <prefix>_0000.rad
./e_<version>_<platform> –i <arguments> <prefix>_0001.rad

Обратитесь к Расширенному руководству по установке базового моделирования для получения информации об использовании PRADIOS с программным обеспечением MPI.

Коды выхода Starter и Engine

Starter и Engine предоставляют коды выхода, которые могут использоваться сценариями.

Значения:

0: Нормальное прекращение.
2: Ошибка модели или расчета.
3 или 128 + номер сигнала: Сбой процесса (дамп ядра, ошибка сегментации).

В Linux код ошибки устанавливается операционной системой: 136 (исключение с плавающей запятой) или 139.

(ошибка сегментации). Код выхода можно получить с помощью команды «$?». в сценарии оболочки Linux:

#!/bin/bash
s_2021.1_linux64 –input [Starter_input]_0000.rad –np 96
Exit_code=$?
echo $Exit_code

В Windows используйте переменную "errorlevel" в скрипте:

s_2021.1_win64.exe –input [Starter_input]_0000.rad –np 96
echo %errorlevel%

Аргументы стартовой командной строки

PRADIOS Starter поддерживает следующие аргументы командной строки.

Аргумент	Короткая форма	Описание
`-help`	`-h`	Распечатать справочное сообщение
`-version`	`-v`	Распечатать информацию о выпуске PRADIOS
`-input [FILE]`	`-i`	Установить входной файл PRADIOS Starter
`-nspmd [INTEGER]`	`-np`	Установить количество доменов SPMD
`-nthread [INTEGER]`	`-nt`	Установить количество потоков на домены SPMD
`-notrap`		Отключить перехват ошибок
`-check`		Возможность проверить модель. Отключите декомпозицию домена и перезапустите запись файла.
`-outfile= [outputpath]`		Определяет каталог выходного файла для всех созданных файлов.
`-HSTP_WRITE`		Напишите `<root_name>_0000.rad2hst` файл содержащий модельную информацию `/PARAMETER`.
`-HSTP_READ`		Считайте файл `hst_input.hstp` и замените входную колоду `/PARAMETER` на те, которые определены в файле `.hstp`.
`-rxalea [REAL]`		Активация узлового случайного шума с помощью [значения] `xalea.`
`-rseed [REAL]`		Необязательное значение: установите `начальное` значение для узлового случайного шума.
`-dylib [FILE]`		Установите имя динамической библиотеки для пользовательских подпрограмм PRADIOS.
`-mds_libpath [PATH]`		Задайте путь к динамической библиотеке для Multiscale Designer.

-help Argument

Выводит справочную информацию об аргументах командной строки.

PRADIOS Starter закрывается после распечатки.

-version Argument

Печатает информацию о выпуске PRADIOS.

Напечатанная информация включает в себя:

Название PRADIOS
Название Радфлекс
Версия для использования
Информация о сборке (дата, время сборки и тег сборки). PRADIOS Starter закрывается после распечатки.

-input [FILE] Argument

Устанавливает входной файл PRADIOS Starter.

Аргумент FILE должен быть входным файлом PRADIOS Starter с именем следующий формат: ``[ROOTNAME]_[RUN NUMBER].rad

где:

ROOTNAME — это корневое имя набора данных.

RUN NUMBER — это номер запуска, выраженный четырьмя числами.

e.g. CRA2V51_0000.rad
ROOTNAME: CRA2V51
RUN NUMBER: 0000

Примечание:

ROOTNAME и RUN NUMBER извлекаются из входного файла.
Настройки набора данных ROOTNAME и RUN NUMBER в /BEGIN_ игнорируются, когда используется опция команды -input.
Если имя файла имеет неправильный формат, файл отклоняется.
Файл открыт. Стандартный ввод больше не используется.
Если -input не установлен, PRADIOS Starter открывает стандартный ввод для чтения ввода.

Пример:

[user@machine]$ ./s_2021.1_linux64 -input CRA2V51_0000.rad

-nspmd [SPMD DOMAIN NUMBER] Argument

Устанавливает количество доменов SPMD.

Где:

SPMD DOMAIN NUMBER: ЦЕЛОЕ число — количество доменов SPMD.

Пример:

[user@machine]$ ./s_2021.1_linux64 -nspmd 4

Примечание:

Если значение SPMD DOMAIN NUMBER установлено неправильно, PRADIOS Starter останавливается с сообщением об ошибке.
Если установлен -nspmd, количество доменов, заданное во входной карточке /SPMD, игнорируется. Карточку /SPMD можно опустить, если другие параметры сохранены как настройки по умолчанию.
Общее количество процессов, используемых для вычислений PRADIOS Engine, будет равно SPMD DOMAIN NUMBER * SMP THREAD NUMBER.

-nthread [SMP THREAD NUMBER] Argument

Устанавливает количество потоков SMP на домен SPMD. Каждый домен SPMD будет вычисляться с использованием многопоточного процесса, состоящего из SMP THREAD NUMBER.

Где SMP THREAD NUMBER: INTEGER — это количество потоков SMP на домен SPMD.

Пример::

[user@machine]$ ./s_2021.1_linux64 -nthread 2

Примечание:

Если значение SMP THREAD NUMBER установлено неправильно, PRADIOS Starter останавливается с сообщением об ошибке.
Если установлен -nthread, количество потоков, заданное во входной карте /SPMD_, игнорируется. Карточку /SPMD можно опустить, если другие параметры сохранены как настройки по умолчанию.
Общее количество процессов, используемых для вычислений PRADIOS Engine, будет равно SPMD DOMAIN NUMBER * SMP THREAD NUMBER.

-notrap Argument

Отключает перехват ошибки PRADIOS Starter.

По умолчанию в случае ошибки PRADIOS Starter выдаст сообщение об ошибке. сообщение, соответствующее произошедшей ошибке, и остановитесь должным образом. Если -notrap используется, PRADIOS Starter продолжит работу и потенциально станет ядром дампа, где возникает ошибка. Такое поведение иногда помогает отследите ошибку с помощью внешних инструментов.

Общее поведение, обработка ошибок

-version
-help
-nspmd, -input, -nthread, -notrap

Примечание: Аргументы 1, 2 и 3 нельзя использовать вместе.: -nspmd, -nthread, -notrap и -input могут использоваться вместе; и порядок не имеет значения.

Если возникает ошибка типа:

Отсутствует аргумент для -input или -nspmd или -nthread
Аргумент -input не является форматом файла PRADIOS.
Аргументы -nspmd или -nthread не являются целочисленным значением.
использован неизвестный аргумент командной строки

Сообщение об ошибке распечатывается вместе с распечатками -help.

-check Argument

Возможность остановки стартера после проверки модели.

Расчет декомпозиции домена и запись файлов перезапуска. (.rst) не выполнено. Это сокращает время запуска модели Starter. запускаться при проверке модели.

-outfile=[output path] Argument

Starter записывает все выходные файлы и файлы перезапуска в определенный выходной путь.

Выходной путь может быть абсолютным или относительным. Если в пути вывода есть пробел, в пути необходимо использовать кавычки. В Windows между каталогами можно использовать «/» или «\».

Пример

Linux:

s_2022_linux64 -i TENSI36_0000.rad -outfile=/storage/files/run1
s_2022_linux64 -i TENSI36_0000.rad -outfile="../my directory"
s_2022_linux64 -i TENSI36_0000.rad -outfile="/storage/files/my directory"

Windows:

s_2022_win64.exe -i TENSI36_0000.rad -outfile=c:\\storage\\files\\run1
s_2022_win64.exe -i TENSI36_0000.rad -outfile="../my directory"
s_2022_win64.exe -i TENSI36_0000.rad -outfile="c:/storage/files/my directory"

-HSTP_WRITE Argument

Запишите файл с именем <root_name>_0000.rad2hst, содержащий всю информацию о параметрах модели (/PARAMETER), определенную в модели (_0000.rad).

Файл <root_name>_0000.rad2hst для HyperStudy с schema=”Laduga_pdd” и schemaVersion=”hstp_v_5”.

-HSTP_READ Argument

Замените значения параметров (/PARAMETER), определенные в модели (_0000.rad), на значения, считанные в файле hst_input.hstp.

Файл hst_input.hstp представляет собой XML-файл для HyperStudy с schema=”Laduga_pdd” и schemaVersion=”hstp_v_5”.

-rseed [seed] Argument

Возможность определить начальное значение для случайного шума в координате узла со значением [seed], реальным значением от 0 до 1.

-rxalea [xalea] Argument

Возможность инициализировать случайный шум в координатах узла значением [xalea], положительным действительным значением.

-dylib [FILE] Argument

Возможность добавить имя файла с полным или относительным путем к пользовательским функциям PRADIOS для выполнения PRADIOS.

-mds libpath [PATH] Argument

Возможность указать путь к динамической библиотеке для законов материалов Multiscale Designer. По умолчанию PRADIOS использует путь, определенный в среде HyperWorks.

Аргумент командной строки механизма

Исполняемые файлы HMPP PRADIOS Engine доступны (начиная с версии 11.0) с MPI и полностью поддерживают гибридное смешивание распараллеливания SPMD и SMP.

Также существуют упрощенные исполняемые файлы, которые поддерживают только SMP, но не требуют MPI.

Чтобы легко различать эти два типа исполняемых файлов, исполняемые файлы MPI имеют суффикс _mpp.

Двоичные файлы, скомпилированные с помощью MPI, необходимо запускать с помощью команды mpirun. Общая форма следующая:

mpirun [список опций mpirun] engine_executable_mpp [список опций движка]

Примечание: Список опций mpirun зависит от поставщика MPI. Обратитесь к документации MPI.

Для двоичных файлов, скомпилированных без MPI:
```
engine_executable [список опций движка]
```

Примечание: Список опций PRADIOS Engine одинаков для обоих типов исполняемых файлов.

PRADIOS Engine поддерживает следующие аргументы командной строки. Каждый аргумент имеет длинную и краткую форму. Это исполняемые аргументы.

Аргумент	Короткая форма	Описание
`-help`	`-h`	Распечатать справочное сообщение
`-version`	`-v`	Распечатать информацию о выпуске PRADIOS
`-input [FILE]`	`-i`	Установить входной файл PRADIOS Engine
`-nthread [INTEGER]`	`-nt`	Установить количество потоков SMP на домен SPMD
`-notrap`		Отключить перехват ошибок
`-norst`		Отключить перезапуск *.rst записи файла во время и в конце вычислений.
`-outfile= [output path]`		Определяет каталог выходного файла для всех созданных файлов.
`-dylib [FILE]`		Установите имя динамической библиотеки для пользовательских подпрограмм PRADIOS.
`-mds_libpath [PATH]`		Задайте путь к динамической библиотеке для Multiscale Designer.

-help Argument

Выводит справочную информацию об аргументах командной строки.

PRADIOS Engine закрывается после распечатки.

-version Argument

Печатает информацию о выпуске PRADIOS.

Информация включает в себя:

Название PRADIOS

Имя Radflex

Версия для использования

Информация о сборке (дата, время сборки и тег сборки)

После распечатки PRADIOS Engine завершает работу.

-input [FILE] Argument

Устанавливает входной файл PRADIOS Engine.

Аргумент FILE должен быть входным файлом PRADIOS Engine со следующими параметрами: формат: [ROOTNAME]_[RUN NUMBER].rad

где:

ROOTNAME — это корневое имя набора данных.

RUN NUMBER — это номер запуска, выраженный четырьмя числами.

Примечание:

ROOTNAME и RUN NUMBER извлекаются из входного файла.
Настройки набора данных ROOTNAME и RUN NUMBE``R в /RUN_ игнорируются, когда используется опция команды ``-input.
Если имя файла имеет неправильный формат, файл отклоняется.
Файл открыт. Стандартный ввод больше не используется.
Если -input не установлен, PRADIOS Engine открывает стандартный ввод для чтения ввода.

Пример

[user@machine]$ mpirun -np 4 ./e_2019_linux64 impi -nt 2 -input CRA2V51_0001.rad
************************************************************************
**                                                                    **
**                                                                    **
**                      PRADIOS ENGINE 2019                           **
**                                                                    **
**             Non-linear Finite Element Analysis Software            **
**                  from Laduga Engineering, Inc.                     **
**                                                                    **
**                                                                    **
**              Linux 64 bits, Intel compiler, Intel MPI              **
**                                                                    **
**                                                                    **
**                                                                    **
**                   Build tag: 0479348_2413000                       **
************************************************************************
** COPYRIGHT (C) 1986-2019           Laduga Engineering, Inc.         **
** All Rights Reserved. Copyright notice does not imply publication.  **
** Contains trade secrets of Laduga Engineering Inc.                  **
** Decompilation or disassembly of this software strictly prohibited. **
************************************************************************
ROOT: CRA2V51 RESTART: 0001
NUMBER OF HMPP PROCESSES 8
17/10/2008
NC=           0 T= 0.0000E+00 DT= 1.7916E-03 ERR= 0.0% DM/M= 0.0000E+00
        ANIMATION FILE: CRA2V51A001 WRITTEN
NC=          100 T= 1.7826E-01 DT= 1.7700E-03 ERR= 0.0% DM/M= 0.0000E+00
...
NC=      13700 T= 1.9871E+01 DT= 1.4032E-03 ERR= -1.2% DM/M= 0.0000E+00

                        ** CPU USER TIME **

#PROC CONT.SORT CONT.F ELEMENT MAT KIN.COND INTEGR. I/O TASK0 ASSEMB RESOL
1 .0000E+00 .0000E+00 .1144E+02 .2910E+01 .7000E-01 .5600E+00 .3100E+00 .5000E+00 .3700E+00 .1364E+02
2 .0000E+00 .0000E+00 .1102E+02 .2870E+01 .7000E-01 .5600E+00 .0000E+00 .0000E+00 .3300E+00 .1364E+02

ELAPSED TIME : 7.79 s

   RESTART FILE: CRA2V51_0001_0000.rst WRITTEN
   NORMAL TERMINATION
   TOTAL NUMBER OF CYCLES: 13793
[user@machine]$

-nthread [SMP THREAD NUMBER] Argument

Устанавливает количество потоков SMP на домен SPMD. Каждый домен SPMD будет вычисляться с использованием многопоточного процесса, состоящего из SMP THREAD NUMBER.

Где SMP THREAD NUMBER: INTEGER — это количество потоков SMP на домен SPMD.

Пример

[user@machine]$ mpirun -np 4 ./e_2019_linux64 impi -nthread 2 -input CRA2V51_0001.rad

Примечание:

Если значение INTEGER установлено неправильно, PRADIOS Starter останавливается с сообщением об ошибке.
если установлен -nthread, количество потоков, определенное при запуске Starter (карта ввода /SPMD, командная строка -nthread) или предыдущем запуске Engine игнорируется.
Переменная среды OMP_NUM_THREADS также может использоваться для изменения количества потоков. -nthread остается до OMP_NUM_THREADS.
Из соображений производительности рекомендуется использовать OMP_NUM_THREADS вместо -nt. Это информирует систему об истинном количестве используемых потоков.
Общее количество процессов, используемых для вычислений PRADIOS Engine, будет равно SPMD DOMAIN NUMBER * SMP THREAD NUMBER.

Общее поведение, обработка ошибок

-version
-help
-input, -nthread, -notrap

Порядок аргументов в командной строке не имеет значения.

Если возникает ошибка типа:

Отсутствует аргумент для -input или -nthread
Аргумент -input не является форматом файла PRADIOS.
Аргумент -nthread не является целым числом

Сообщение об ошибке распечатывается вместе с распечатками -help.

Согласованность опций MPI и PRADIOS

Значение -nspmd (или поле Nspmd входной карты /SPMD Starter) должно соответствовать значению mpirun -np. Если это не так, PRADIOS Engine остановится с соответствующим сообщением об ошибке.

Пример неправильных команд:

[user@machine]$ ./s_2019_linux64 -nspmd 4 -input CRA2V51_0000.rad

[user@machine]$ mpirun -np 2 ./e_2019_linux64 impi -input CRA2V51_0001.rad

В этом случае PRADIOS отобразит сообщение об ошибке в стандартном выводе и файле листинга:

THE REQUIRED NUMBER OF MPI PROCESSES DOES NOT MATCH MPIRUN
   PLEASE, RUN с THE PROPER NUMBER OF MPI PROCESSES
   REQUIRED (NSPMD) = 4
   AVAILABLE (mpirun -np) = 2
   E R R O R T E R M I N A T I O N
   TOTAL NUMBER OF CYCLES : 0

Пример правильных команд:

[user@machine]$ ./s_2019_linux64 -nspmd 4 -input CRA2V51_0000.rad
[user@machine]$ mpirun -np 4 ./e_2019_linux64 impi -input CRA2V51_0001.rad

-notrap Argument

Добавьте эту опцию для принудительного дампа ядра.

Это полезная опция для получения обратной трассировки стека вызовов.

-norst Argument

Возможность отключить перезапуск записи файла *.rst во время и в конце вычислений.

Это заставляет движок работать быстрее из-за уменьшения количества записываемых файлов.

-outfile=[output path] Argument

Механизм записывает все выходные файлы и файлы перезапуска по определенному пути вывода.

Выходной путь может быть абсолютным или относительным. Если в пути вывода есть пробел, в пути необходимо использовать кавычки. В Windows между каталогами можно использовать «/» или «\».

Пример

Linux:

e_2022_linux64 -i TENSI36_0000.rad -outfile=/storage/files/run1
e_2022_linux64 -i TENSI36_0000.rad -outfile="../my directory"
e_2022_linux64 -i TENSI36_0000.rad -outfile="/storage/files/my directory"

Windows:

e_2022_win64.exe -i TENSI36_0000.rad -outfile=c:\\storage\\files\\run1
e_2022_win64.exe -i TENSI36_0000.rad -outfile="../my directory"
e_2022_win64.exe -i TENSI36_0000.rad -outfile="c:/storage/files/my directory

-dylib [FILE] Argument

Возможность добавить имя файла с полным или относительным путем к пользовательским функциям PRADIOS для выполнения PRADIOS.

-mds libpath [PATH] Argument

Возможность указать путь к динамической библиотеке для законов материалов Multiscale Designer. По умолчанию PRADIOS использует путь, определенный в среде HyperWorks.

Процесс решения

Моделирование PRADIOS состоит из двух частей: стартера и двигателя. Стартер представляет собой проверку входных данных и должен успешно завершиться без ошибок, прежде чем моделирование может быть завершено в двигателе.

Starter и Engine

PRADIOS Starter принимает в качестве входных данных модель или обычно называемый входной файл Starter runname_0000.rad и создает выходной файл Starter runname_0000.out. PRADIOS Starter отвечает за проверку согласованности модели и сообщает о любых ошибках или предупреждениях в выходном файле. Если в модели нет ошибок, PRADIOS Starter создает исходный файл(ы) перезапуска runname_0000_CPU#.rst. Для каждого домена SPMD MPI, запрошенного для решения, создается один файл перезапуска.

Вторая часть вычислений PRADIOS называется PRADIOS Engine. PRADIOS Engine принимает в качестве входных данных файл PRADIOS Engine runname_0001.rad и начальные файлы перезапуска, созданные PRADIOS Starter. Файлы PRADIOS Engine описывают управление решением и выходные данные для моделирования. Во время работы PRADIOS Engine создается выходной файл Engine, runname_0001.out, который содержит статистику моделирования, включая время, временной шаг, текущие энергии системы, энергетическую ошибку и массовую ошибку.

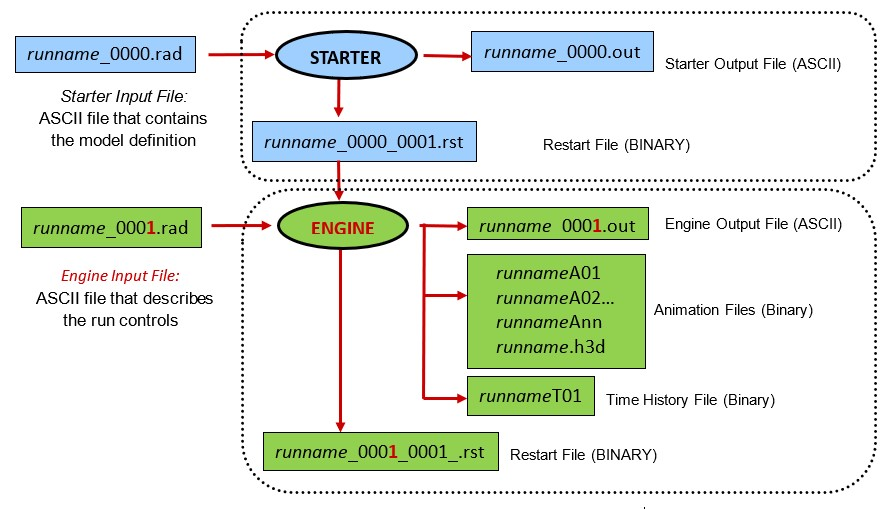
Фигура 2: Процесс расчета PRADIOS при использовании одного домена MPI

Требования к памяти и диску

Память выделяется автоматически PRADIOS Starter, а используемый объем указан в выходном файле Starter.

STARTER MEMORY USAGE 1486 MB

Затем Starter дает оценку памяти и размер файла перезапуска для каждого процесса MPI.

LOCAL ENGINE STORAGE EVALUATION FOR SPMD PROCESSOR 1
-------------------------------------------------------
MEMORY USED FOR REALS 80 MB
MEMORY USED FOR INTEGERS 35 MB
TOTAL MEMORY EVALUATION 115 MB
RESTART FILE SIZE 60091KB
...
LOCAL ENGINE STORAGE EVALUATION FOR SPMD PROCESSOR 18
-------------------------------------------------------
MEMORY USED FOR REALS 83 MB
MEMORY USED FOR INTEGERS 38 MB
TOTAL MEMORY EVALUATION 122 MB

RESTART FILE SIZE 63349KB

После завершения работы PRADIOS Engine выходной файл Engine содержит подробную информацию о фактической памяти и дисковом пространстве, используемых симуляцией.

               ** MEMORY USAGE STATISTICS **

TOTAL MEMORY USED .........................: 10284 MB
MAXIMUM MEMORY PER PROCESSOR...............: 605 MB
MINIMUM MEMORY PER PROCESSOR...............: 562 MB
AVERAGE MEMORY PER PROCESSOR...............: 571 MB

                ** DISK USAGE STATISTICS **

TOTAL DISK SPACE USED .....................: 1421485 KB
ANIMATION/TH/OUTP SIZE ....................: 200950 KB
RESTART FILE SIZE .........................: 1220535 KB

Одна рабочая станция

Используйте только SPMD, указав опцию запуска -np NumDomains.
NumDomains должно быть количеством ядер, доступных в процессоре рабочей станции.
Если для ЦП включена поддержка Hyperthreading, компьютер будет иметь в два раза больше ядер, чем указано в спецификации ЦП. Эти дополнительные ядра являются виртуальными и поэтому обеспечивают лишь небольшое ускорение. За счет использования этих дополнительных ядер можно получить ускорение на 5 %, но будут использоваться дополнительные лицензии, поскольку количество лицензий зависит от количества запрошенных ядер. При использовании гиперпоточности гибридный режим с двумя потоками SMP, -nt 2, даст наилучшее ускорение. Например, если используется 8-ядерный процессор, PRADIOS -nt 2 -np 8 model_0000.rad.

Компьютерный кластер

Когда количество используемых ядер < 256, самое быстрое время решения можно получить, используя только SPMD через -np NumDomains. Обратите внимание на значение по умолчанию -nt =1, поэтому его не нужно включать.
Когда количество используемых ядер > 256, следует использовать гибридный режим, -nt NumThreads -np NumDomains. NumThreads= 2 и NumDomains= (# используемых ядер)/2.

Например, если узел кластера содержит 2 ЦП, каждый из которых имеет 8 ядер. Чтобы использовать 512 ядер, NumThreads=2 и NumDomains = 512/2=256.
Все ядра, доступные на вычислительном узле, должны быть использованы и выделены для решения PRADIOS, то есть, если вычислительный узел имеет 16 ядер, то количество доступных для использования ядер должно быть кратно 16.
В решении не следует использовать ядра Hyperthreading и, если возможно, гиперпоточность можно отключить в биосе системы.

Для управления кластером рекомендуется использовать планировщик заданий, например Laduga PBS.

Две или три рабочие станции

Возможно использование двух или трех рабочих станций, подключенных по гигабиту. Ethernet для решения одной симуляции PRADIOS.

Для достижения наилучших результатов все машины должны иметь идентичное аппаратное обеспечение или, по крайней мере, иметь один и тот же процессор и быть подключены к гигабитному Ethernet или более быстрой сети.
Гибридный режим можно использовать для минимизации сетевого взаимодействия, `` np`` NumDomains -nt NumThreads. Начните с установки NumThreads=2 и NumDomains=(общее количество ядер, доступных на всех машинах)/NumThreads. Запустите эталонную модель и сравните время запуска модели на одной рабочей станции.
Затем увеличьте значение NumThreads и повторно запустите тест, чтобы увидеть, есть ли дополнительное ускорение. NumThreads должно быть ≤ количества ядер на 1 процессоре. Число доменов должно быть кратно числу используемых компьютеров.

Например, если вы используете две рабочие станции с двумя процессорами каждая, и каждый процессор имеет 8 ядер. Доступно 2*2*8=32 ядра.

◦ -nt 2 -np 16 = OK

◦ -nt 4 -np 8 = OK

◦ -nt 8 -np 4 = OK
Если для процессоров включена технология Hyper-Threading, не используйте дополнительные ядра Hyper-Threading.

Требуется дополнительная настройка, как описано в Расширенном руководстве по установке Laduga Simulation.

Размер модели

При использовании нескольких ядер для решения задачи моделирования должно быть разумное количество элементов.

Хороший баланс между ускорением и эффективностью достигается за счет наличия в модели не менее 10 000 элементов для каждого ядра, используемого в решении. Итак, для модели с 320 000 элементов 320 000/10 000 = 32 ядра. Обычно дополнительное ускорение можно получить вплоть до 1000 элементов на ядро.

Используйте другое количество ядер

Стартер может использовать несколько ядер посредством распараллеливания SMP.

Для очень больших моделей, которые будут работать с использованием большого количества доменов SPMD, Starter будет работать быстрее, если для декомпозиции домена и создания файлов перезапуска будет использоваться несколько ядер SMP. При использовании Compute Console (ACC) или включенного скрипта Starter и Engine необходимо запускать отдельно с использованием опции -onestep. Например, предположим, что очень большая модель из 3 миллионов элементов будет работать на 120 ядрах вычислительного сервера с 12 ядрами на ЦП.

Стартер будет использовать 12 ядер для расчета 120 доменов SPMD и создания файлов перезапуска.

PRADIOS -nt 12 -np 120 -onestep model_0000.rad

Движок будет использовать 120 ядер с использованием распараллеливания SPMD.

PRADIOS -nt 1 -np 120 -onestep model_0001.rad

Передовые методы

Существуют различные расширенные методы, которые могут быть полезны для проверки состояния моделирования, остановки моделирования, изменения некоторых параметров моделирования или использования одинарной точности.

Управляющий файл (C-файл)

Дополнительный управляющий файл используется для получения информации о текущем анализе.

Во время моделирования может быть очень полезно получить больше информации, чем указано в выходном файле Engine. Это можно сделать с помощью файла управления PRADIOS, который имеет то же префиксное имя, что и текущий входной файл Engine, но заканчивается на *.ctl. Если текущий работающий файл Engine называется TensileTest_0001.rad, то управляющий файл должен называться TensileTest_0001.ctl.

Некоторые причины использовать контрольный файл включают в себя:

Получить текущее состояние моделирования, включая текущее время моделирования, временной шаг, цикл, информацию об энергии и расчетное оставшееся время.
Остановить вычисления немедленно или в указанное время или номер цикла.
Создание анимации немедленно или в указанное время или номер цикла.

Если моделирование запускается в вычислительной консоли Laduga с отмеченными параметрами управления решателем, появится следующее диалоговое окно, и управляющий файл будет создан автоматически с использованием выбранных параметров при нажатии кнопки Отправить команду.

Рисунок 3:

Если вычислительная консоль (ACC) не используется, управляющий файл можно создать с помощью текстового редактора и сохранить в каталоге, в котором PRADIOS записывает выходной файл Engine.

В управляющем файле доступны следующие параметры, причем каждый параметр размещается на отдельной строке. Если не указан параметр /TIME или /CYCLE, действие выполняется сразу после того, как PRADIOS прочитает управляющий файл. В противном случае действие выполняется в указанное время /TIME или /CYCLE.

Действие

Результат

/ANIM

Создайте дополнительный файл анимации (A###). Выходная частота, определенная в файле Engine, не изменится при использовании этой опции.

/CHKPT

Создайте файл с именем CHECK_DATA, который содержит команды /RERUN_ для продолжения моделирования, если оно остановлено. Обычно используется в сочетании с /STOP_ для остановки моделирования. Недоступно с неявным решением.

/CYCLE/Nbcycle

команды управляющего файла будут выполняться с указанным номером цикла.

/H3D

запись данных анимации в файл *.h3d. Выходная частота, определенная в файле Engine, не изменится при использовании этой опции.

/INFO

Возвращает информацию о текущем цикле, текущих глобальных энергиях, текущем временном шаге. Эта информация пишется всегда для всех опций.

/KILL

завершить симуляцию и не создавать файл перезапуска.

/RFILE

Создайте файл перезапуска.

/STOP

Остановить симуляцию и создать файл перезапуска, чтобы его можно было перезапустить.

/TIME/timeValue

Остальные команды управляющего файла будут выполнены в указанное время моделирования.

Когда PRADIOS обнаруживает файл управления, текущий статус моделирования записывается в тот же файл управления с использованием введенных параметров.

Например, моделирование выполняется в удаленной системе и поэтому не запускается с помощью вычислительной консоли Laduga. Поскольку входной файл Engine называется «TensileTest_0001.rad», создается управляющий файл с именем «TensileTest_0001.ctl» со следующей информацией и загружается в рабочий каталог моделирования.

/TIME/.1
/ANIM
/CHKPT
/STOP

Когда PRADIOS обнаруживает файл управления, в тот же файл TensileTest_0001.ctl записывается следующая информация с информацией о текущем состоянии моделирования и выполнении команд файла управления. При t=0,1 в симуляции PRADIOS создаст файл анимации, файл CHECK_DATA, файл перезапуска и остановит симуляцию.

RUN CONTROL FILE
-------------------
WRITE NEXT ANIMATION FILES AT TIME 0.1000000
WRITE NEXT RESTART FILE AT TIME 0.1000000
RUN STOP AT TIME 0.1000000

CURRENT STATE:
-------------
CYCLE     = 13040
TIME      = 0.8153611E-02
TIME STEP = 0.6252749E-06SOLID     70
ENERGY ERROR       = 0.0%
INTERNAL ENERGY    = 0.1188329E-02
KINETIC ENERGY     = 0.1050914E-07
ROT. KIN. ENERGY   = 0.000000
EXTERNAL WORK      = 0.1188431E-02
MASS.ERR (M-M0)/M0 = 0.000000

CURRENT ELAPSED TIME     = 4.88 s
REMAINING TIME ESTIMATE  = 594.04 s

Несколько файлов движка

Можно определить несколько файлов Engine, чтобы изменить управление решением и выходные данные во время моделирования.

Некоторые распространенные случаи использования этой мощной функции включают в себя:

Инициализация силы тяжести или предварительного натяжения перед симуляцией.
Изменение частоты записи выходных файлов, таких как файлы анимации (/ANIM/DT, /H3D/DT), история времени (/TFILE) и перезапуск (/RFILE ).
Изменение используемых параметров управления временным шагом (/DT/Keyword).
Изменение системного демпфирования (/DAMP, /DYREL или /KEREL).
Добавление или удаление граничных условий (/BCS/Keyword) или определение начальных условий (/INIV/Keyword).
Удаление элементов (/DEL/Eltyp) или включение или выключение твердых тел (/RBODY/Keyword2).

Определите и запустите несколько входных файлов механизма

Как упоминалось выше, первый файл Engine называется runname_0001.rad. При создании второго файла Engine число для следующего файла Engine увеличивается на 1 до максимального числа 9999 файлов Engine. Таким образом, второй файл Engine будет называться runname_0002.rad. Чтобы избежать появления предупреждающего сообщения, номер файла Engine также должен совпадать с номером запуска, указанным в ключевом слове /RUN.

Пример: файл первого движка «TensileTest_0001.rad».

/RUN/TensileTest/1
5.0
/TFILE
0.005
/ANIM/DT
0. 0.5
/ANIM/TENS/STRESS/MEMB
/PRINT/-1000
/DT/NODA/CST
0.9 1e-6

Пример: файл второго движка TensileTest_0002.rad с измененными параметрами.

/RUN/TensileTest/2
10.0
/TFILE
0.0005
/ANIM/DT
0. 0.05
/ANIM/TENS/STRESS/MEMB
/PRINT/-10
/DYREL
1.00 0.002
/DT/NODA/CST
0.9 1e-7

Смотрите также

RD-E: 1200 Jumping Bicycle

Файл контрольной точки

Файл контрольных точек используется для продолжения остановленного моделирования.

Если в файл Engine не требуется вносить никаких изменений, остановленное моделирование PRADIOS можно продолжить, используя файл контрольных точек с именем CHECK_FILE, содержащий параметр /RERUN/Имя запуска/Номер запуска. CHECK_FILE можно создать с помощью текстового редактора или остановив моделирование с помощью вычислительной консоли (ACC), опций управления решателем STOP и CHKPT.

CHECK_FILE можно создать с помощью текстового редактора, скопировав исходный файл Engine с именем CHECK_FILE, изменив строку /RUN на /RERUN и удалив все остальные строки из файла. П ри использовании Laduga Compute Console или сценария PRADIOS для перезапуска решения файл Starter или Engine можно выбрать в качестве входного файла и использовать те же параметры ввода и количество процессоров, которые были определены ранее, а также добавить параметр -checkpoint. . Например, PRADIOS

-np 4 -checkpoint tensileTest_0000.rad

При запуске PRADIOS напрямую с исполняемыми файлами в качестве входных данных для исполняемого файла Engine следует указать CHECK_FILE.

Вычисление одинарной точности

Версия PRADIOS с одинарной точностью называется расширенной одинарной точностью, поскольку большинство вычислений выполняются с одинарной точностью, но некоторые остаются с двойной точностью для получения более точного результата.

По умолчанию PRADIOS использует формат с плавающей запятой двойной точности при выполнении вычислений, в отличие от других явных решателей, которые по умолчанию используют одинарную точность. В формате двойной точности используется точность от 15 до 17 значащих десятичных цифр; тогда как в формате одинарной точности используется точность от 6 до 9 значащих десятичных цифр.

Хотя версия с одинарной точностью зависит от модели, она работает на 30–40 % быстрее, чем версия с двойной точностью.

Когда в вычислениях используется одинарная точность, в вычислениях с плавающей запятой возникает больше ошибок округления из-за меньшего количества значащих цифр в одинарной точности. Поскольку явные вычисления рассчитывают один цикл за раз, а следующий цикл основан на вычислениях предыдущих циклов, моделирование с большим количеством циклов может накапливать ошибку округления по мере продвижения моделирования, что приводит к менее точному результату.

Чтобы свести к минимуму ошибку округления, рекомендуется использовать версию PRADIOS по умолчанию, которая имеет двойную точность. Это наиболее важно в симуляциях, которые имеют следующие характеристики:

Большее количество циклов решения из-за малого шага по времени или длительного времени моделирования.
Небольшой размер элемента
Моделирование подушек безопасности
Неявное моделирование
Жидкость и жидкость - Моделирование взаимодействия структур, ALE, CEL
Высокоскоростное воздействие, такое как баллистическое моделирование.

Самый простой способ определить, даст ли моделирование точные результаты с помощью вычислений с одинарной точностью, — это сравнить результаты одинарной точности с результатами двойной точности, чтобы выявить любые большие различия. Результаты одинарной и двойной точности не будут идентичны, но они должны быть очень близки.

Запустите симуляцию с одинарной точностью

При использовании Compute Console (ACC) версию с одинарной точностью можно запустить с помощью опции -sp.

PRADIOS -np 24 -sp tensile_model_0000.rad

При непосредственном использовании исполняемых файлов PRADIOS версия с одинарной точностью запускается с использованием исполняемых файлов, которые включают имя «_sp» как для PRADIOS Starter, так и для двигателя.

./s_<version>_<platform>_sp –i <prefix>_0000.rad ./e_<version>_<platform>_sp –i <prefix>_0001.rad

Смотрите также

Запустите PRADIOS (FAQ)

Явный структурный анализ методом конечных элементов

В этом разделе представлены доступные явные функции для различного явного анализа.

Шаг времени

Явная задача решается путем вычисления результатов с небольшими временными приращениями или шагами по времени. Размер временного шага зависит от многих факторов, но автоматически рассчитывается PRADIOS.

Результаты рассчитываются для каждого временного шага или цикла моделирования. Следовательно, чем меньше временной шаг, тем больше времени потребуется для решения моделирования, поскольку выполняется больше циклов и вычислений. Как обсуждалось в разделе «Динамический анализ» Руководства по теории радиоизлучения, для решения уравнений движения используется метод интегрирования по направлениям. Метод прямого интегрирования, используемый в PRADIOS, основан на схеме интегрирования по времени Ньюмарка. Этот метод решает уравнения движения, используя пошаговую процедуру с использованием численно стабильного шага по времени, $\Delta t$. Численная устойчивость незатухающих систем`_ Теории PRADIOS

Руководство показывает, что система без демпфирования останется устойчивой, если $\Delta t\leq\frac{2}{\omega_{\text{max}}}$. Где $\omega_{\text{max}}$ — самая высокая угловая частота в системе. Для дискретного моделирования методом конечных элементов решение остается устойчивым, если ударная волна, проходящая через сетку, не проходит через более чем один элемент за один временной шаг. Таким образом, ударная волна не пропускает ни одного узла при прохождении через сетку и, таким образом, возбуждает все частоты в сетке конечных элементов. Используя скорость звука в материале $c$ и характеристическую длину $l_{c}$ конечного элемента, время прохождения волны по длине одного элемента составит:

\[\Delta t=\frac{l_{c}}{c} \tag{1}\]

Чтобы дискретное решение оставалось устойчивым, шаг по времени должен быть меньше или равен времени, необходимому для прохождения волны через один элемент:

\[\Delta t\leq\frac{l_{c}}{c} \tag{2}\]

Этот критерий устойчивости часто называют условием Куранта в честь исследования, впервые проведенного Курантом и др. в 1928 году. ²

Временной шаг элемента

Расчет временного шага по умолчанию, используемый PRADIOS, представляет собой временной шаг элемента.

Для одного конечного элемента шаг по времени элемента можно записать как:

\[\Delta t_{Element}=\frac{l_{c}}{c} \tag{3}\]

Где,

$l_{c}$ Характеристическая длина элемента, расчет которой зависит от типа используемого элемента и описан в разделе Конечные элементы Руководства пользователя.

$c$ Скорость звука в материале, которую можно выразить как $\sqrt{\frac{E}{\rho}}$

$p$ Плотность материала

$E$ Модуль Юнга

Для каждого цикла моделирования характерная длина и скорость звука каждого элемента используются для расчета критического временного шага каждого элемента модели. Расчет шага по времени происходит одновременно с расчетом внутренней силы. Чтобы обеспечить стабильность, шаг времени цикла моделирования определяется путем умножения минимального шага времени всех элементов на масштабный коэффициент (по умолчанию — 0,9). Масштабный коэффициент необходим для обеспечения стабильности моделирования в случае внезапного изменения жесткости модели.

Метод шага по времени элемента применяется ко всей модели с использованием:

/DT

$\Delta T_{sca}\Delta T_{\min}$

Где,

$\Delta T_{sca}$ Масштабный коэффициент для временного шага элемента

$\Delta T{\min}$ Минимальный временной шаг, который активирует определенные действия, перечисленные в /DT

Узловой шаг по времени

Узловой временной шаг вычисляет временной шаг на основе узловой массы и узловой жесткости в модели.

Узловой шаг по времени рассчитывается после расчета всех внутренних сил в каждом узле с использованием:

\[\Delta t_{nodal}=\sqrt{\frac{2m}{k}} \tag{4}\]

Где,

$m$ Узловая масса

$k$ Эквивалентная узловая жесткость

Эквивалентная узловая жесткость рассчитывается с использованием половины собственного значения матрицы жесткости каждого присоединенного элемента. Если узел также участвует в контакте, контактная жесткость также включается в расчет эквивалентной узловой жесткости. Жесткость рассчитывается во время расчета внутренней силы. Чтобы обеспечить стабильность, шаг времени цикла моделирования определяется путем умножения минимального шага времени всех узлов на масштабный коэффициент (по умолчанию — 0,9).

Для высококачественной сетки конечных элементов условия шага по времени элемента и шага по узловому времени практически идентичны. Большинство типичных сеток конечных элементов включают некоторые элементы с низким качеством элементов, и в таких ситуациях расчет узлового шага по времени обычно выше, чем расчет временного шага элемента.

Метод узлового временного шага применяется ко всей модели с использованием:

/DT/NODA

$\Delta T_{sca}\Delta T_{\text{min}}$

Где,

$\Delta T_{sca}$ Масштабный коэффициент для временного шага элемента

$\Delta T_{\text{min}}$ Не используется и вводится как ноль.

Смотрите также

/DT/NODA/Keyword3/Iflag (Engine)

Глобальный временной шаг

Метод глобального временного шага (GTS) можно использовать для расчета временного шага модели на основе собственной частоты модели.

Для некоторых моделей метод глобального временного шага приводит к более высокому временному шагу по сравнению с расчетом временного шага на основе каждого элемента или узла. Для расчета глобального временного шага используется итерационный алгоритм, который обходится дороже, чем расчет элементарного или узлового временного шага. Таким образом, расчет глобального временного шага по умолчанию выполняется каждые 20 циклов.

/DT/GLOB/Iflag

$\Delta T_{sca}$

If Iflag=1, вставьте следующую строку

Tol_GTS Ncycles

Где,

$\Delta T_{sca}$ Масштабный коэффициент для временного шага элемента

Tol_GTS

Допуск сходимости для итеративного алгоритма.

Ncycles

Число циклов между расчетом глобального временного шага.

Метод глобального времени полезен в моделях без больших изменений в жесткость, например, при моделировании испытаний на падение.

Параметр «Глобальный временной шаг» доступен для следующих функций:

Сплошные элементы: /TETRA4, /TETRA10, шестнадцатеричные с флагами ниже.
/PROP/SOLID: $I_{solid}$ = 1 (Беличко), 14 (HA8), 17 (H8C), 24 (HEPH) и 16 (20-узловой)
Элементы оболочки: $I_{shell}$ = 1 (Белычко-Цай), 12 (Батоз) и 24 (ГЭПХ)
Элемент фермы
Элемент балки
Контактные интерфейсы: TYPE7, TYPE24 (без опции «от края до края») и TYPE2 с $Spot_{flag}$ =25 и 27.

Временной шаг контактного интерфейса

Временной шаг контактного интерфейса рассчитывается двумя разными способами. Во-первых, на основе жесткости, а во-вторых, на основе скорости вторичных узлов.

Временной шаг контактного интерфейса, основанный на жесткости, рассчитывается только для TYPE 7, TYPE 10, TYPE 11, TYPE 19, TYPE 21, TYPE 24 и TYPE 25. Независимо от того, какой метод временного шага используется, узлы, участвующие в контактах, имеют повышенную жесткость, что приводит к необходимости расчета временного шага узлового контакта с использованием узловой массы, жесткости интерфейса и жесткости элемента.

\[\Delta t_{inter;nodal}=\sqrt{\frac{2M_{nodal}}{\sum\left(K_{interface}+K_{element}\right)}} \tag{5}\]

Где,

$M_{nodal}$ Узловая масса

$K_{interface}$ Жесткость интерфейса

$K_{element}$ Жесткость элемента

Кинематический шаг времени контакта интерфейсов TYPE7, TYPE11 и TYPE19 используется, чтобы гарантировать, что вторичный узел не проникнет за пределы основного сегмента в течение одного цикла:

\[\Delta t_{kin}=\frac{1}{2}\Bigg{[}\frac{Gap-p}{\frac{dp}{dt}}\Bigg{]} \tag{6}\]

Где,

$Gap$ Контактный разрыв

$p$ Сумма проникновения

${\frac{dp}{dt}}$ Относительная скорость проникающего вторичного узла (или линии для контакта TYPE11) относительно основного сегмента (или линии для контакта TYPE11).

Выходные данные временного шага из модели

Временной шаг исходной модели выводится в выходной файл Starter. Тогда как временной шаг работающей модели можно выводить в файлы анимации.

Начальный временной шаг модели

Доступны различные методы для определения временного шага модели. Некоторые препроцессоры могут рассчитывать и отображать временной шаг сетки. При выполнении PRADIOS Starter временной шаг, основанный на элементе

типы и узлы записаны в выходном файле Starter runname_0000.out. Эти значения временного шага рассчитываются с использованием приведенных выше формул и не включайте масштабный коэффициент временного шага.

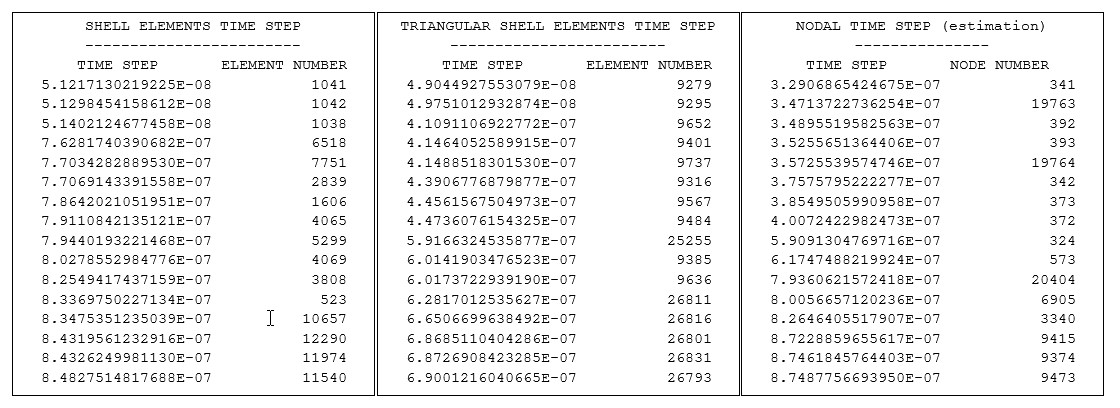
Рисунок 4: Расчет временного шага в стартовом выходном файле

Гистограмма, показывающая распределение узлового шага по времени в модели, также печатается в выходном файле Starter.

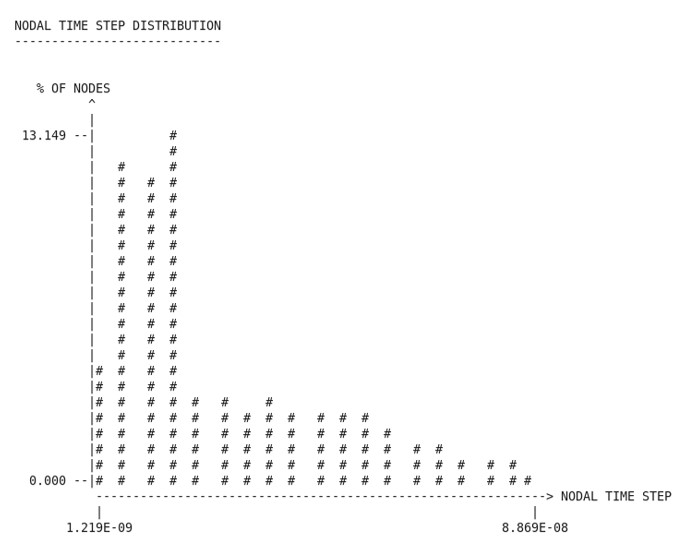
Рисунок 5: Гистограмма распределения узловых временных шагов

Шаг выполнения модели по времени

Когда PRADIOS Engine работает, узловой временной шаг также можно записать в выходные файлы анимации, используя параметр вывода /ANIM/NODA/DT или /H3D/NODA/DT. Временной шаг элемента доступен с помощью /ANIM/ELEM/DT или /H3D/ELEM/DT. Затем файл анимации можно построить в HyperView по контуру, чтобы наблюдать временной шаг элементов в моделировании.

Временной шаг также можно просмотреть в выходном файле Engine. Частоту можно установить с помощью /PRINT/#, где временной шаг записывается каждые # циклов, или информацию о временном шаге текущего цикла можно вывести с помощью команды /INFO в /INFO Управляющий файл (файл C).`_

Если используется временной шаг элемента, тип элемента и идентификатор элемента с минимальным временным шагом будут напечатаны в выходном файле Engine. Если в модели есть контактный интерфейс, узел или интерфейс могут быть указаны как имеющие минимальный временной шаг и описаны в разделе «Методы управления временным шагом».

Временной шаг, управляемый элементом

CYCLE   TIME     TIME-STEP    ELEMENT   ERROR
     0.000    0.2043E-03    SHELL      202   0.0%
  0.2043   0.2043E-03    SHELL      201   0.0%
  0.4086   0.2043E-03    SHELL      201   0.0%
  0.6129   0.2043E-03    SHELL      201   0.0%
  0.8171   0.2043E-03    SHELL      201   0.0%

Если используется узловое управление временным шагом, в выходном файле Engine обычно будет указано, что УЗЕЛ управляет временным шагом, и будет указан идентификатор узла. `тип временного шага, используемого при вычислении`_ описывает ситуацию, когда временной шаг, основанный на контактной жесткости, является минимальным временным шагом в моделировании, основанном на:

\[\Delta t_{{inter;nodal}}=\sqrt{\frac{2M_{{nodal}}}{\sum\left(K_{{interface}}+K_{{element}}\right)}} \tag{7}\]

Временной шаг, управляемый узлом

CYCLE   TIME        TIME-STEP    ELEMENT    ERROR
     0.000        0.5317E-06   NODE       20404    0.0%
  0.5317E-03   0.5317E-06   NODE       20404    0.0%
  0.1063E-02   0.5317E-06   NODE       20404    -0.4%
  0.1595E-02   0.5317E-06   NODE       20404    -1.0%
  0.2127E-02   0.5317E-06   NODE       20404    -0.9%

Если кинематический временной шаг контактного интерфейса имеет минимальный временной шаг в модели, в выходном файле Engine будет указано, что INTER управляет временным шагом, и будет указан идентификатор контактного интерфейса. Когда это происходит, вторичные узлы контактного интерфейса движутся так быстро, что они пройдут через основную контактную поверхность за один цикл временного шага, и, таким образом, чтобы этого не произошло, временной шаг моделирования уменьшается. Шаг времени, сделанный в /DT/INTER/DEL. предоставляет более подробную информацию.

Временной шаг, управляемый контактным интерфейсом

CYCLE    TIME T       IME-STEP       ELEMENT     ERROR
      0.000        0.1093E-04      INTER       35 0.0%
   0.1093E-4    0.1093E-04      INTER       35 0.0%
   0.2186E-4    0.1093E-04      INTER       35 0.0%
   0.3279E-4    0.1093E-04      INTER       35 0.0%
   0.4372E-4    0.1093E-04      INTER       35 0.0% %

Методы управления временным шагом

Шаг по времени часто можно увеличить, используя некоторые из этих методов управления шагом по времени.

Одной из наиболее распространенных проблем при явном моделировании методом конечных элементов является количество времени, необходимое для решения моделирования. Чем больше временной шаг модели, тем меньше циклов требуется для решения моделирования, что приводит к меньшему времени решения.

Если не учитывать контактную жесткость, минимальный временной шаг моделирования является функцией размера сетки, жесткости и плотности материала. Поэтому первый способ увеличить временной шаг модели — улучшить качество сетки путем модификации элементов с небольшой длиной ребра относительно средней длины элемента сетки.

После улучшения сетки другой распространенной проблемой является уменьшение шага по времени из-за деформации сетки. Как упоминалось ранее, минимальный шаг по времени рассчитывается во время каждого цикла моделирования, и по мере возникновения деформации размер элементов может уменьшаться, что приводит к уменьшению шага по времени. Если происходит значительное уменьшение шага по времени,

С некоторыми небольшими изменениями все эти методы используют этот формат ввода.

/DT/option/Keyword3/Iflag

$\Delta T_{sca}\Delta T_{\min}$

Где,

$\Delta T_{sca}$ Масштабный коэффициент для критического узлового шага по времени

$\Delta T_{\min}$ Минимальный временной шаг модели, который активирует управление временным шагом

Для всех параметров управление временным шагом активируется, когда $\Delta T_{\min}\geq\Delta T_{sca}*\Delta t_{option};$ где, $\Delta t_{option}$ — это расчет временного шага на основе используемого параметра, такого как узел, элемент или интерфейс.

Лагранжевы элементы, объем которых становится отрицательным во время моделирования, автоматически переключаются на формулы деформации, что позволяет продолжить моделирование. В этом случае в выходном файле Engine будет напечатано предупреждающее сообщение.

Таблица 1: Поддерживаемые опции

тип элемента и формулировка

Состав штамма

Метод обработки отрицательного объема

/BRICK, Isolid =1,

2, 14, 17, 24

/TETRA4, Itetra = 0

/TETRA10

Полные геометрические

нелинейности Ismstr =2, 4

Переключитесь на малую деформацию, используя форму элемента из

цикла до отрицательного объема.

Общая деформация типа Лагранжа

Ismstr = 10, 12

Общая деформация типа Лагранжа с формой

элемента в момент времени = 0,0

Автоматическое переключение на малую нагрузку можно отключить, установив для Keyword2 значение STOP в /NEGVOL_.

Узловое управление шагом времени

Узловое управление шагом времени активируется для моделирования с помощью опции:

/DT/NODA/Keyword3/Iflag

$\Delta T_{sca}\Delta T_{\min}$

С временным шагом узла в сетке, определяемым как:

\[\Delta t_{nodal}=\sqrt{\frac{2m}{k}} \tag{8}\]

Где,

$m$ Узловая масса

$k$ Эквивалентная узловая жесткость

Примечание: Если масса узла увеличивается или жесткость уменьшается, то временной шаг моделирования увеличивается.

По умолчанию узловой временной шаг применяется ко всей модели. Если Iflag=1, то после масштабного коэффициента и временного шага вводится дополнительная строка с идентификатором набора узлов группы. Это можно использовать для применения узлового управления временным шагом к группе узлов /GRNOD, которые были определены в Starter.

Примечание: Независимо от того, какая опция Keyword3 используется, в файле Engine одновременно можно использовать только одну опцию /DT/NODA/Keyword3/Iflag. Если включено несколько, используется только последний.

/DT/NODA/CST

/DT/NODA/CST на сегодняшний день является наиболее популярным вариантом сохранения или увеличения временного шага моделирования. PRADIOS автоматически добавит массу к узлам, чтобы сохранить введенное значение. При необходимости масса будет добавлена в начале моделирования, чтобы соответствовать введенному значению.

Преимущества и недостатки

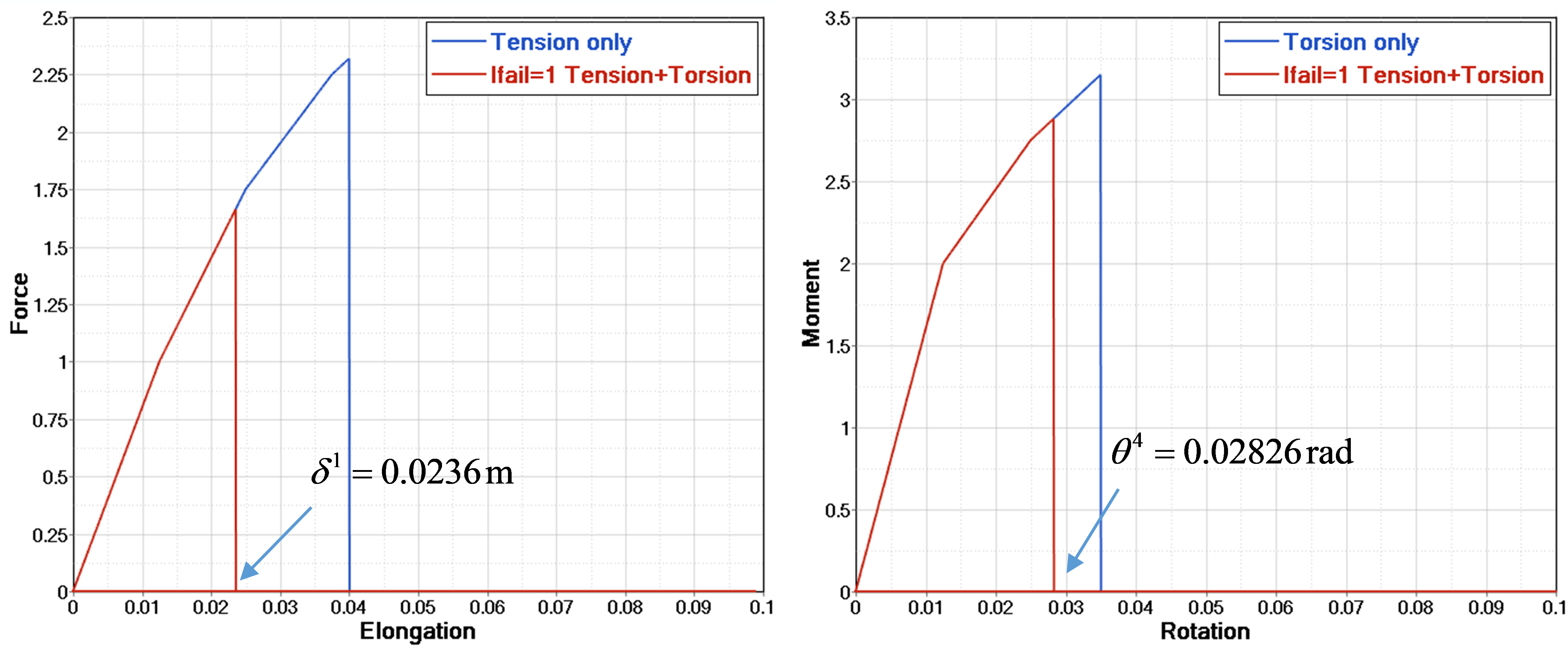
Увеличение узловой массы с помощью /DT/NODA/CST — это самый простой способ увеличить временной шаг модели или предотвратить падение временного шага ниже определенного значения во время моделирования. Чтобы определить, какую массу можно добавить к модели, необходимо использовать хорошее инженерное решение. Добавление слишком большого количества массы может повлиять на физику за счет увеличения кинетической энергии при моделировании падения или удара. Это связано с тем, что моделируемый объект весит больше реальной части. Увеличение массы также может изменить поведение модели на высоких частотах, что может быть очень важно при ударах на очень высокой скорости, таких как баллистика или взрывы.

В общем, рекомендуется поддерживать количество добавляемой массы на уровне менее 5%. Однако в некоторых типах моделирования может быть приемлемо большее увеличение массы. Например, в квазистатическом моделировании скорости обычно малы, поэтому добавление массы не приводит к значительному увеличению кинетической энергии. По этим причинам рекомендуется проверить увеличение массы в модели, запустив моделирование без или с уменьшенным масштабированием массы и сравнив результаты. Если добавленная масса приводит к добавленной кинетической энергии, энергетическая ошибка, рассчитанная PRADIOS, будет положительной.

Выберите временной шаг для массового масштабирования

Чтобы определить, сколько массы будет добавлено в модель, PRADIOS вычисляет целевой шаг по времени для различных величин процентного увеличения массы. Целевой временной шаг рассчитывается для процентного увеличения массы от 0,5% до 10% для масштабных коэффициентов временного шага $\Delta T_{sca}$, равных 0,9 и 0,67. Эта информация печатается в виде таблицы и графика в выходном файле Starter.

Примечание: Эта оценка действительна только для первого цикла. Добавленная масса может увеличиться во время пробега из-за деформации элементов или контактов, что означает, что добавленная масса может превысить значение, ожидаемое по оценке Стартера.

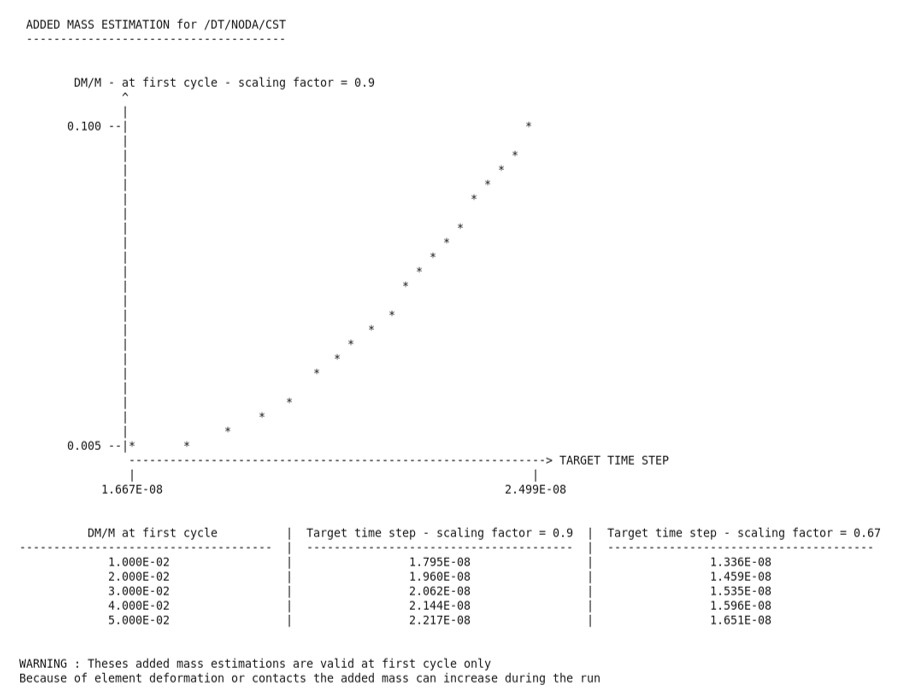
Рисунок 6: Добавленная масса для разных целевых временных шагов

Целевой временной шаг и масштабный коэффициент затем можно использовать в /DT/NODA/CST.

Проверьте увеличение массы

Общее увеличение массы указано в выходном файле двигателя в последнем столбце под названием «MAS.ERR». Используя опцию вывода анимации /ANIM/NODA/DMASS или /H3D/NODA/DMASS, относительное увеличение массы на узел можно визуализировать в постпроцессоре в виде контурного графика. Как общая ошибка массы, так и ошибка узловой массы представляют собой изменение массы, деленное на исходную массу в начале моделирования.

\[MASSERR\text{or}DMAS=\left(\frac{DM}{M_{0}}\right) \tag{9}\]

С, ${DM}=M-{M_{0}}$

Где,

${M_{0}}$ Начальная масса в начале моделирования для каждого файла Engine.

$m$ Текущая масса

Примечание: Начальная масса сбрасывается в начале каждого моделирования файла Engine, а общее увеличение массы должно быть добавлено из всех выходных файлов Engine.

Можно построить кривые массы и энергии глобальной временной истории, чтобы понять, как увеличение массы влияет на моделирование.

Примечание: Вывод массы детали с использованием /TH/PART не включает добавленную массу из-за массового масштабирования.

/DT/NODA/SET

Уменьшает эквивалентную узловую жесткость ($k$) для сохранения введенного значения $\Delta T_{\min}$. Это снижение жесткости также меняет физику моделирования и обычно используется только при моделировании жидкостей.

/DT/NODA/STOP

Останавливает симуляцию, когда временной шаг симуляции падает ниже введенного значения $\Delta T_{\min}$. Во многих случаях уменьшение шага по времени вызвано нестабильностью модели, поэтому остановка моделирования может быть полезна для диагностики проблемы.

Управление шагом времени элемента

Временной шаг элемента можно контролировать с помощью параметров Engine:

/DT/Eltyp/Keyword3/Iflag

$\Delta T_{sca}\Delta T_{\min}$

Где,

Eltype тип элемента

Keyword3 Используемый тип управления временным шагом

Если Iflag=1, то для некоторых TYPEов элементов и методов управления временным шагом вводится вторая строка с дополнительным вводом.

Для всех параметров Ключевое слово3 предпринятое действие произойдет при расчете временного шага элемента, определенного в Конечные элементы. Для управления временным шагом элемента доступна только одна опция Keyword3 для каждого Eltyp, что означает, что невозможно использовать /DT/BRICK/CST и /DT/BRICK/DEL в та же модель, но /DT/SHELL/STOP и /DT/BRICK/CST могут использоваться вместе.

/DT/Eltyp/CST

Eltyp=BRICK or SHELL.

Эта опция управляет временным шагом, переключая элементы на формулу малой деформации, если они приводят к тому, что временной шаг моделирования становится меньше $\Delta T_{min}$. Это происходит только при использовании определенных значений $I_{smstr}$, определенных в определении свойства /PROP для элемента. Хотя переход к формулировке с малой деформацией не так точен, как с большой деформацией, снижение точности часто необходимо для получения решения в разумные сроки.

Если используется /DT/BRICK/CST/1, добавляется вторая дополнительная строка.

$\Delta T_{sca}\Delta T_{\min}$

ASP_min VDEF_min

Где,

ASP_min Минимальный аспект

VDEF_min Минимальный коэффициент объема $(V/{V_{0}})$

Элементы будут переключены на режим малой деформации, когда будет достигнуто одно из двух минимальных значений ASP_min или VDEF_min. ASP_min использует тот же расчет схлопывания tet, что и проверка качества элемента HyperMesh. Элементы, не соответствующие критериям ASP_min, будут переведены на формулу малой деформации в начале или во время моделирования. VDEF_min можно использовать для переключения сильно деформированных или сжатых элементов на формулу малой деформации во время моделирования, что позволяет избежать проблем с отрицательным объемом, которые иногда возникают во время моделирования.

Когда происходит переход к формулировке малых деформаций, предполагается постоянная матрица Якоби, и все пространственные переменные (характеристические длины, объемы и т. д.) рассматриваются в их исходной конфигурации. На этом этапе деформация элемента больше не учитывается при расчете шага по времени. Если скорость звука постоянна, шаг по времени становится и остается постоянным. Согласно некоторым законам твердого материала, скорость звука зависит от давления. Поэтому возможно, что шаг по времени станет немного меньше, чем $\Delta T_{\min}$. Если временной шаг элемента меньше $\Delta T_{\min}$ в начале моделирования, то элемент переключится на формулировку малой деформации и, предполагая, что элемент имеет наименьший временной шаг, будет запущено моделирование. с шагом по времени меньше $\Delta T_{\min}$. Когда элемент переключается на формулировку малой деформации, в выходной файл двигателя выводится сообщение.

Преимущества и недостатки

Переход к формулировке малой деформации останавливает уменьшение шага по времени, которое, если позволить ему продолжать, приведет к тому, что моделирование будет выполняться намного дольше. В большинстве случаев небольшая потеря точности, вызванная использованием нескольких элементов в формуле малой деформации, стоит того, чтобы гарантировать получение результатов в разумные сроки. Переход на малую деформацию лучше, чем добавление массы и, следовательно, кинетической энергии при динамическом моделировании или удаление элемента и, таким образом, удаление кинетической энергии. Переключение на малую деформацию для сохранения шага по времени может быть лучшим решением в динамическом моделировании, а не добавлением или потерей кинетической энергии, связанной с добавлением массы или удалением элементов.

Для элементов оболочки ограничений меньше, чем для сплошных элементов. В аварийных приложениях основной деформацией оболочки является изгиб, и формулировка малой деформации не влияет на описание изгиба, если деформация мембраны мала.

Большое количество элементов, переходящих на формулировку малой деформации, обычно указывает на проблему модели, которую необходимо изучить.

/DT/Eltyp/DEL

Удаляет элемент, из-за которого шаг времени моделирования становится меньше $\Delta T_{\min}$. Когда элементы удаляются, физика модели меняется, поскольку удаление элемента изменяет массу, инерцию и, возможно, жесткость модели. Когда элемент удаляется, сообщение печатается в выходной файл Engine.

/DT/Eltyp/STOP

Останавливает симуляцию, когда временной шаг симуляции падает ниже введенного значения $\Delta T_{\min}$. Во многих случаях уменьшение шага по времени вызвано нестабильностью модели, поэтому остановка моделирования может быть полезна для диагностики проблемы.

Контактный интерфейс управления временным шагом

Шагом времени контактного интерфейса можно управлять с помощью опций Engine:

/DT/INTER/Keyword3/Iflag

$\Delta T_{sca}\Delta T_{\min}$

Для всех параметров Keyword3 предпринятое действие произойдет, когда $\Delta T_{\min}\geq\Delta T_{sca}\ast\Delta t_{interface}$ где, $\Delta t_{interface}=\min(\Delta t_{inter,modab}\Delta t_{kin})$ — это минимальный временной шаг контактной жесткости и кинетический временной шаг, как определено в `_ Временной шаг контактного интерфейса`_. Если Iflag=1, то вторая строка с дополнительным вводом вводится для /DT/INTER/AMS.

Примечание: Этот элемент управления используется только с контактными интерфейсами с нелинейной жесткостью TYPE7, TYPE10, TYPE11, TYPE19 и TYPE21.

/DT/INTER/CST

Автоматически увеличивает массу узлов, участвующих в контакте, для сохранения введенного значения. Обычно эта опция бесполезна, поскольку вторичные узлы контакта с малыми временными шагами обычно имеют высокую степень проникновения в контактный зазор, а при добавлении массы их кинетическая энергия увеличивается, что приводит к увеличению проникновения и, таким образом, нестабильности модели. Количество добавленной массы должно отслеживаться во время и проверяться после моделирования таким же образом, как /DT/NODA/CST.

/DT/INTER/DEL

Удаляет узлы, участвующие в контактном интерфейсе, из-за которых временной шаг моделирования падает ниже $\Delta T_{\min}$. Эта опция может быть очень полезна для поддержания заданного шага по времени, но если количество удаленных узлов слишком велико, то контакт будет некорректным, и результаты могут быть неточными.

/DT/INTER/STOP

Останавливает симуляцию, когда временной шаг контактного интерфейса падает ниже введенного значения $\Delta T_{\min}$. Во многих случаях уменьшение шага по времени вызвано нестабильностью модели, поэтому остановка моделирования может быть полезна для диагностики проблемы.

/DT/INTER/AMS

Применяет расширенное массовое масштабирование к вторичным узлам интерфейса для поддержания постоянного шага по времени, $\Delta T_{\min}$. Дополнительную информацию см. в разделе «Расширенное массовое масштабирование (AMS)».

Расширенное массовое масштабирование (РММ)

Смотрите также
/AMS (Starter)
/DT/AMS (Engine)-
`RD-E: 4400 Blow Molding с AMS`_

Увеличьте скорость вычислений и поддерживайте точность

AMS (Advanced Mass Scaling) существенно экономит время вычислений за счет увеличения временного шага модели для явных вычислений. Это похоже на традиционное масштабирование массы, за исключением того, что добавленная масса не увеличивает поступательную кинетическую энергию системы.

Недиагональная матрица масс используется для увеличения шага по времени в каждой строке матрицы масс. Сосредоточенная масса M0 увеличивается с некоторым значением M, компенсируемым недиагональными членами, так что общая масса остается постоянной. ¹ В отличие от традиционного массового масштабирования, AMS изменяет только высокие частоты и существенно не влияет на низкие частоты модели.

Преимущество AMS по сравнению с традиционным масштабированием массы, управляемым пользователем, заключается в том, что поступательная кинетическая энергия не увеличивается. Это позволяет увеличить шаг по времени до существенно более высоких значений по сравнению с традиционным массовым масштабированием без существенного влияния на качество результатов.

Поскольку AMS не изменяет глобальную массу даже на больших временных шагах, глобальный импульс узлов, на которые влияет AMS, сохраняется. На больших временных шагах традиционные /DT/NODA/CST могут добавить к вычислениям значительную массу, что увеличивает поступательную кинетическую энергию.

У AMS есть вычислительные затраты, связанные с вычислением матрицы масс. Вычислительные затраты зависят от модели, но для сильно нелинейной модели они могут составлять 50% от общих вычислительных затрат. Таким образом, хотя стоимость цикла выросла, количество циклов расчета сокращается, за счет увеличенного шага по времени. Например, при использовании шага по времени в 10 раз больше традиционного /DT/NODA/CST общее время расчета сократилось в 3 раза. Следовательно, чтобы увидеть разумное сокращение затраченного времени, нужно в 10 раз рекомендуемой отправной точкой является временной шаг /DT/NODA/CST.

Вычислительная сходимость и точные результаты могут быть получены, если установить целевой временной шаг в 10–20 раз выше, чем при традиционном массовом масштабировании. В производственном моделировании можно использовать временной шаг, в 50 раз превышающий традиционный шаг массового масштабирования. Поскольку условие Куранта по-прежнему необходимо соблюдать, устойчивость модели должна быть достигнута с заданным шагом по времени для применения AMS.

Несколько модификаций модели могут помочь повысить ее устойчивость при большом временном шаге. Ниже приведены некоторые рекомендации и предложения, позволяющие обеспечить стабильность модели.

Примечание: Advanced Mass Scaling специфичен для PRADIOS. Он является продвинутым, поскольку его можно применять ко всей модели без ухудшения производительности вычислений и качества результатов.

14.0 Новые функции AMS

Совместимость с RBE2 и RBE3

13.0 Новые функции AMS

Совместимость с движущимися жесткими стенами (/RWALL с node_ID > 0)
Исправлены фиксированные жесткие стены (/RWALL с node_ID = 0 или пустым)
Значение допуска по умолчанию изменено с 1E-4 на 1E-3 (Tol_AMS = 0 # 0,001)
Улучшены критерии сходимости сопряженного градиента (CG).
Оптимизирована матрица недиагональной добавленной массы.

Примечание: Допуск AMS был изменен, чтобы компенсировать небольшую потерю производительности по времени вычислений из-за вышеперечисленных улучшений, но это не должно повлиять на точность результатов.

Starter

Только ключевое слово

Только /AMS должен присутствовать, чтобы применить AMS либо к назначенной группе деталей, либо ко всей модели, если за ним следует пустая строка (вход PRADIOS Starter).

ВНИМАНИЕ: /DT/AMS является обязательным для ввода PRADIOS Engine, за которым следует масштабный коэффициент и целевой увеличенный шаг времени для активации AMS (PRADIOS Engine Input). Без /DT/AMS в файле Engine, /AMS в стартовом файле игнорируется.

HMPP / SPMD

Если для DOMDEC установлено значение 0, Starter по умолчанию указывает на 3 (многоуровневое разложение Kway). Вплоть до версии 11.0.230, если применяется /AMS, DOMDEC необходимо вручную переключить на 5 (многоуровневое разложение Kway на основе DOF). Начиная с версии 11.0.240, Starter автоматически устанавливает для DOMDEC значение 5, если оно установлено в 0 и если /AMS присутствует, в противном случае для DOMDEC будет установлено значение 3, если /АМС отсутствует.

Интерфейсы

Рекомендуется использовать флаг жесткости интерфейса $I_{\textit{strf}}=4K=\max\bigl{[}St_{\min}\min\bigl{(}St_{\max},K_ {n}\bigr{)}\bigr{]}$ с $K_{n}=\min\bigl{(}K_{m},K_{s}\bigr{)}$ и масштабным коэффициентом жесткости Stfac = 1 (значение по умолчанию) для контактных интерфейсов TYPE7, TYPE11 и TYPE19.
Если задействовано трение, рекомендуется установить тип формулировки штрафа за трение, $I_{form}$, равным 2 (дополнительная жесткость для кулоновского трения), всякий раз, когда эта опция доступна (/INTER/TYPE7 и /TYPE19.
Для AMS, как и при стандартном масштабировании массы, рекомендуется не иметь трения в контакте TYPE11, если контакт TYPE7 (уже обрабатывающий трение) уже определен для тех же деталей. Это позволяет избежать падения шага по времени и помогает моделировать сходимость. Эта рекомендация становится устаревшей, если трение TYPE11 использует $I_{form}$ =2 для межкраевых контактов, начиная с версии 13.0.
При контактных интерфейсах TYPE7, TYPE11 и TYPE19, использующих нелинейную штрафную жесткость для контакта, может потребоваться использование опции /DT/INTER/DEL во входной панели PRADIOS Engine. В противном случае AMS может медленно сходиться или расходиться.

Моранке, Лайонел и Жерар Винкельмюллеры. «Динамическая конденсация и выборочное масштабирование массы в PRADIOS Explicit». 19-й французский конгресс механиков (2009 г.).

Использование /DT/INTER/AMS бессмысленно при использовании /DT/AMS, но /DT/INTER/AMS может использоваться вместо ``/DT/NODA/CST. `` когда контакты сильно влияют на временной шаг.
Начальные пересечения и проникновения должны быть удалены, насколько это возможно (а также традиционное массовое масштабирование, особенно если оно используется для сравнения с результатами AMS).

ВНИМАНИЕ: Барьеры, другие элементы воздействия и, в частности, манекены содержат множество интерфейсов, которые НЕ подлежат изменению, поскольку их проверка основана на исходных параметрах /INTER (в случае изменения их проверка не гарантируется).

Твердые тела

Инерция малых твердых тел должна быть скорее сферической, если для $I_{math{sphere}}$ установлено значение 1.

ВНИМАНИЕ: Манекены содержат множество небольших твердых тел, которые НЕ следует изменять, поскольку их проверка основана на исходных параметрах /RBODY (в случае изменения их проверка не гарантируется).

Летающие узлы: не являются ограничением, но их следует удалить, а также несвязанные небольшие твердые тела, которые не нужны.
Рэлеевское демпфирование: в некоторых случаях, когда упругая область остается большой в ходе моделирования, могут наблюдаться плохие характеристики AMS с зашумленными кривыми зависимости времени (пример, сила-время) и шаблонами Арлекина на контурных графиках (пример, фон Мизес). Значительное улучшение должно произойти при вставке карты демпфирования Рэлея (/DAMP в стартовом файле), влияющей на детали, подверженные AMS, с использованием следующих параметров:

$\alpha=0$ и $\beta=0.05\Delta t_{\mathit{AMS}}$

(где $\Delta t_{\mathit{AMS}}$ — это целевой временной шаг AMS, поэтому $\beta$ — это 5%-кратный целевой временной шаг AMS). Такая модификация может позволить увеличить целевой временной шаг AMS для значительного улучшения характеристик AMS.

Примечание: Здесь не рекомендуется использовать числовое демпфирование (dm или Навье-Стокса) вместо демпфирования Рэлея.

Engine

Только ключевое слово: только /DT/AMS должно присутствовать, чтобы вызвать AMS с целевым увеличенным элементарным шагом времени (вход PRADIOS Engine).

ВНИМАНИЕ: /AMS является обязательным во входе PRADIOS Starter для обозначения выбранных деталей или всей модели, к которой применяется AMS.

В /DT/AMS/Iflag, если $I_{\mathit{flag}}$ = 1, должен быть предусмотрен допуск на сходимость AMS, ToLAMS. Если $I_{\mathit{flag}}$ игнорируется, применяется значение по умолчанию (1E-3) для ToLAMS. Не рекомендуется изменять допуск AMS, если в этом нет необходимости. Обратите внимание, что ToLAMS был 1E-4 в версии 12.0.210.

В /DT/AMS/Iflag, если $I_{\mathit{flag}}$ = 2, отображение количества итераций AMS может помочь в отладке или мониторинге сходимости без дополнительных затрат на процессор. Максимально допустимое количество итераций перед отправкой сообщения о расхождении по умолчанию составляет 1000. Рекомендуется НЕ менять это значение. Если значение превышает это максимальное значение, PRADIOS останавливается со следующим сообщением об ошибке:

** ERROR ** AMS is LIKELY DIVERGING

Мониторинг количества итераций за цикл может помочь понять результирующую производительность AMS:
От 75 до 100 итераций — признак действительно плохой сходимости. 50 итераций могут не обеспечить никакого ускорения. 30 итераций или меньше считаются хорошей сходимостью.

В качестве масштабного коэффициента рекомендуется использовать 0,67, $\Delta T_{sca}$, а не 0,9 (как и в традиционном масштабировании узловых масс /DT/NODA/CST, особенно если это используется для сравнения с результатами AMS).

Задайте минимальный шаг по времени, $\Delta T_{min}$, от 10 до 20 раз, чем тот, который используется в /DT/NODA/CST, то есть начните с 10 раз, затем проверьте, как еще многое предстоит сделать, проверив численную сходимость, выигрыш затраченного времени и качество результатов.

/DT/AMS не будет изменять глобальную массу, поэтому:

Глобальный импульс связанных узлов сохраняется.
Сравнение с традиционным масштабированием массы требует незначительного добавления массы при вычислении /DT/NODA/CST, если оно используется в качестве эталона.

/DT/Eltyp/Keyword3 совместим с /DT/AMS, за исключением /DT/INTER/CST (дополнительную информацию см. в разделе «Возможности и ограничения»).

Используйте /DT/INTER/DEL в качестве обходного пути для медленной сходимости или возможного расхождения при вызове нелинейной штрафной жесткости с контактными интерфейсами TYPE7, TYPE11 и TYPE19.

/ANIM/NODA/NDMAS может быть добавлен для вывода недиагонального изменения массы.

/ANIM/NODA/DINER может быть добавлен для вывода добавленной инерции для каждого узла.

Возможности и ограничения

AMS совместим со следующими опциями:

Кинематические условия

Граничные условия: /BCS
Наложенные скорости: /IMPVEL
Навязанные смещения: /IMPDISP
Наложенные ускорения: /IMPACC
Связанные контакты: /INTER/TYPE2 $Spot_{flag}$ 0, 1, 2 (кинематическая формулировка), 25, 27 или 28 (формулировка штрафа)

◦ Твердые тела: /RBODY (при условии, что они не активированы или деактивированы датчиком)

◦ Фиксированные жесткие стены: /RWALL с node_ID= 0 или пустые (в случае трения по-прежнему рекомендуется использовать ударный элемент с жесткой сеткой из-за стоимости AMS).

◦ Перемещение жестких стен: /RWALL с node_ID > 0 (в случае трения по-прежнему рекомендуется использовать ударный элемент с жесткой сеткой из-за стоимости AMS)

◦ Жесткие ссылки: /RLINK

◦ Кинематические соединения: /KJOINT (/PROP/TYPE33) и /KJOINT2 (/PROP/TYPE45)

◦ Цилиндрические соединения: /CYL_JOINT

◦ Активные разделы: /SECT

◦ Скорости: /VEL/TRA или /VEL/ROT

◦ Начальные скорости: /INIV/TRA или /INIV/ROT
Твердые тела можно активировать и деактивировать с помощью ключевых слов /RBODY/ON и OFF в качестве движка.
Жесткие элементы: /RBE2
Элементы ограничения интерполяции: /RBE3

Элементы

Все классическое: фермы, балки, пружины, оболочки и твердые тела.
4-узловая тетра: /TETRA4, только если $I_{tetra10}$ =0
10-узловая тетра: /TETRA10, только если $I_{tetra10}$ =0
Формулировка элемента:

◦ QEPH $I_{shell}$ =24 и все остальные $I_{shell}$ параметры

◦ HEPH $I_{solid}$ =24

Интерфейсы

/DT/AMS совместим с интерфейсами.

TYPE2 (см. Связанные контакты выше)
TYPE7
TYPE10
TYPE11
TYPE19
TYPE21
TYPE24
TYPE25
Динамическое расслабление: /DYREL, /ADYREL
Рэлеевское демпфирование: /DAMP
/DT/Eltyp/Keyword3 совместим с /DT/AMS

Сюда входит /DT/Eltyp/CST, для которого формула малой деформации активируется для элемента, когда

$\Delta T_{sca}$ $\cdot\frac{l}{c}<$ $\Delta T_{\min}$ tag{10}

Где,

$l$ Характеристическая длина элемента,

$c$ Скорость звука в материале

Применение /DT/AMS к выбранным частям (в /AMS из стартового входного файла) не исключает одновременное использование /DT/NODA/CST,
примененное к частям, не относящимся к AMS. остальная часть модели. Это рекомендуется даже для того,
чтобы минимизировать время вычислений в моделях, где AMS применяется только к выбранным частям.

Примечание. В AMS бессмысленно использовать больший временной шаг, чем тот, который используется в классическом массовом масштабировании, поскольку меньший временной шаг ограничивает производительность.

Подушки безопасности без эталонных показателей должны работать

Смотрите также
`/AMS (Starter)`_
`/DT/AMS (Engine)`_

Ограничения (могут сосуществовать, но вне выбранной группы деталей AMS)

ВНИМАНИЕ: /PARITH/ON еще не застрахован AMS на случай изменения количества доменов. Но для одного и того же номера домена результаты одинаковы независимо от количества потоков.

SPH: AMS не увеличивает временной шаг SPH (пример: раскачивание танка при столкновении)
ALE - Эйлер - FVM: формулировки не поддерживаются (но могут быть вынесены из части /AMS, если временной шаг достаточный)
2D-анализ: /AMS недоступен.
Части, включающие:

◦ Множители Лагранжа: /MPC и /GJOINT

◦ /FXBODY

В таких случаях PRADIOS Engine выдает предупреждение, и вычисления могут даже отклониться.

Элементы:

◦ 4-узловая тетра: /TETRA4 с $I_{tetra4}$ =1 или 3

◦ 10-узловая тетра: /TETRA10 с $I_{tetra10}$ =2

◦ 16-узловая оболочка: /SHEL16

◦ 20-узловые блоки: /BRIC20

◦ Многоцепочечный: /XELEM

В таких случаях расчеты, скорее всего, будут расходиться.

Твердые тела нельзя активировать и деактивировать с помощью датчиков.
Интерфейсы: /DT/INTER/CST не совместим с /DT/AMS

◦ У узлов, которые являются вторичными по отношению к обоим: связанному интерфейсу TYPE2 и контактному интерфейсу (TYPE7 или TYPE11), будет удалена жесткость контакта. Затем будет удалено стартовое сообщение в файле 0.out. изданный:

** WARNING SECONDARY NODE OF AN INTERFACE TYPE2 & AMS

INTERFACE TYPE[7 or 11], ID=xxxxxx: SECONDARY NODE ID=yyyyyyy IS ALSO SECONDARY NODE OF AN INTERFACE TYPE2

THE NODE CONTACT STIFFNESS WILL BE DE-ACTIVATED CASE OF /DT/AMS

Деактивации контакта можно избежать, используя $Spotf_{\text{tag}}$ =25, 27 или 28 (формулировка штрафа TYPE2).

◦ Кинематическая формула (TYPE2) для точечной сварки может изменить характеристики AMS при наличии большого количества точечных сварных швов, особенно шестигранных.

Подушки безопасности со справочными метриками: /REFSTA или /XREF не получают преимущества от ускорения AMS.
См. `Входы стартера`_ и `Входы двигателя`_ Справочные руководства.

Таблица 2: Сводная информация об основных ограничениях расширенного массового масштабирования

	Элементарный временной шаг для AMS `/DT/AMS` во входных данных PRADIOS Engine
Множители Лагранжа	Не работает
16-узловые толстые оболочки и 20- узловые кирпичи	К этим элементам применяется свободный временной шаг элемента.
Твердые тела активируются и деактивируются с помощью датчиков	Не работает
Интерфейсы	Только TYPE2, TYPE7, TYPE10, TYPE11, TYPE19, TYPE20, TYPE21, TYPE24, и TYPE25 поддерживаются

Основные показатели качества

При постоянном узловом управлении шагом времени (/DT/NODA/CST) ошибка энергии (ERROR %) и добавленная масса (MASS.ER) являются первыми, которые проверяются внутри выходного файла (``_0001.out ``).

При использовании AMS добавленная масса не имеет значения. Просмотрите энергетическую ошибку, изменение временного шага и оставшееся количество итераций за цикл.

Общим для обоих подходов являются кривые энергетического баланса.

Точность результатов

Численный эффект AMS на результаты аналогичен снижению высших собственных частот структуры. Поскольку AMS влияет на высокие частоты, он подходит для квазистатического моделирования, испытаний на падение и производственного (штамповочного) моделирования. Не рекомендуется использовать для сильно деформированных конструкций или явлений с высокой скоростью, таких как моделирование взрывов и баллистики. Иногда AMS может использоваться при моделировании аварий, если выборочно применяется к группе деталей конструкции с мелкой сеткой, что потенциально снижает вычислительную производительность всей модели. В таких случаях целевой временной шаг AMS этих выбранных частей (исключая подсистемы безопасности, такие как барьеры, манекены, подушки безопасности и удерживающие системы) должен быть установлен равным значению временного шага остальной части модели, где классическая масса применяется масштабирование.

В большинстве случаев собственные векторы (а затем AMS) не влияют на поведение потери устойчивости. В особых случаях, например, при разрушении коробчатой балки, ширина и амплитуда пиковых усилий могут быть изменены, поскольку пиковая сила может быть не обнаружена из-за более высокого временного шага AMS. Схема выпучивания правильная, но поглощенная энергия на первом пике не одинакова.

Вращение твердых тел: AMS может влиять на инерцию вращения небольших твердых тел. Инерция этих небольших твердых тел будет увеличена, чтобы достичь целевого шага по времени.

При сравнении результатов AMS с эталонным прогоном убедитесь, что добавленная масса в эталонном прогоне достаточно мала, чтобы это не повлияло на результаты.

Уроки выучены

Начиная с постоянного значения узлового временного шага (/DT/NODA/CST, традиционного в производстве) в качестве «эталона» и применяя постепенно увеличивающийся целевой временной шаг AMS (/DT/AMS), было показано четыре этапы, включающие как числовую стабильность, так и качество результата:

Слишком близкое к традиционному значению постоянного узлового временного шага, численная стабильность AMS превосходна и результаты почти идентичны «эталонным». Конечно, ускорение невелико из-за стоимости итерации AMS. Теоретически целевой коэффициент x3 вернет «эффективное ускорение» x1, что не принесет никакой пользы.
Чуть выше предыдущего случая. Числовая стабильность AMS остается удовлетворительной, в основном показывая ссылки на минимальные временные шаги, связанные с элементом (возможные ссылки на интерфейсы). Результаты по-прежнему близки к «эталонным», стоимость итерации AMS амортизируется, а ускорение начинает расти. При расчете целевых коэффициентов от x3 до x10, скорее всего, эффективное ускорение будет варьироваться от x1,5 до x3, а возможно и больше.
Помимо этого, численная стабильность может выглядеть удовлетворительной, возможно, с большим количеством итераций за цикл и большим количеством ссылок на минимальные временные шаги, связанные с интерфейсом. Результаты могут либо выглядеть приемлемыми, либо существенно отличаться от «эталонных». Ускорение продолжает расти, если только интерфейсы на основе штрафов не диктуют минимальный временной шаг, вызывающий увеличение количества итераций и возможное падение временного шага, что влияет на ускорение. Однако целевые коэффициенты от x10 до x20, возможно x30, могут обеспечить эффективное ускорение в диапазоне от 4 до 6, возможно, 9 соответственно (больше было обнаружено при моделировании штамповки), что НЕ следует считать успешным, пока результаты AMS не проверяются и не сравниваются с приведенными выше. определенные «эталонные» результаты.
В предыдущих случаях вычисления либо расходятся, а затем останавливаются с явным сообщением AMS, либо останавливаются из-за предела энергетической ошибки (без добавленной массы), либо временной шаг резко падает, и выполнение необходимо остановить в интерактивном режиме.

Примеры файла 1.out иллюстрируют влияние AMS на выходной файл PRADIOS («1.out») в зависимости от введенного целевого временного шага.

Подсказки

Когда модели содержат детали с очень разными размерами сетки, возможно, лучше применять AMS только к частям, нарушающим временной шаг. Затем, для оптимизации производительности вычислений, рекомендуется также применить классическое массовое масштабирование к частям, не принадлежащим к группе частей /AMS, в противном случае ни одна обработанная AMS часть не будет вычисляться по умолчанию с естественным шагом времени элемента. .

Пример:

/DT/AMS/1
:math:`\Delta T_{sca}\Delta T_{min}`
Tol.AMS
/DT/NODA/CST
:math:`\Delta T_{sca}\Delta T_{min}`

Бессмысленно использовать более высокий временной шаг в AMS, чем тот, который используется в классическом массовом масштабировании, поскольку меньший временной шаг ограничивает производительность. Если группа деталей не указана (пустая строка) или равна 0, то AMS применяется к модели в целом, и добавление /DT/NODA/CST не имеет значения.

Для AMS, как и при стандартном масштабировании массы, рекомендуется не иметь трения в контакте TYPE11, если контакт TYPE7 (уже обрабатывающий трение) уже определен для тех же деталей. Это позволяет избежать падения шага по времени и помогает моделировать сходимость. Эта рекомендация устарела, если трение TYPE11 использует $I_{form}$ =2, доступное для контактов от края до края с версии 13.0.

У узлов, которые являются вторичными по отношению к обоим: связанному интерфейсу TYPE2 и контактному интерфейсу (TYPE7 или TYPE11), будет удалена жесткость контакта. Затем выдается стартовое сообщение в файле 0.out. :

** WARNING SECONDARY NODE OF AN INTERFACE TYPE2 & AMS

INTERFACE TYPE[7 or 11], ID=xxxxxx:

SECONDARY NODE ID=yyyyyyy IS ALSO SECONDARY NODE OF AN INTERFACE TYPE2

THE NODE CONTACT STIFFNESS WILL BE DE-ACTIVATED CASE OF /DT/AMS

Деактивации контакта можно избежать, используя $Spot_{flag}$ =25, 27 или 28 (формулировка штрафа TYPE2).

Кинематическая формула (TYPE2) для точечной сварки может изменить характеристики AMS при наличии большого количества точечных сварных швов, особенно шестигранных.

В некоторых динамических случаях, часто в упругом состоянии, проявляются странные упругие вибрации (показывающие контуры фон Мизеса, похожие на арлекина), вынуждающие снизить целевой временной шаг AMS, что приводит к плохим характеристикам AMS. Эти вибрации можно уменьшить, а целевой временной шаг AMS повторно увеличить для повышения производительности за счет применения демпфирования Рэлея. Рекомендуемое значение демпфирования:

$a$ = 0 и $\beta=0.05\Delta t_{\mathit{AMS}}$ — целевой временной шаг AMS.

Примечание. Начиная с версии 13.0 значение допуска по умолчанию было изменено с 1E-4 на 1E-3 (Tol_AMS = 0 # 0,001).

Смотрите также
`/AMS (Starter)`_
`/DT/AMS (Engine)`_

Пример: автомобильная промышленность

Для автомобильных приложений разумным значением для начала является целевой шаг по времени, равный 10-кратному эталонному (узловому постоянному) шагу по времени. Однако были успешно использованы шаги, превышающие эталонный временной интервал более чем в 20 раз.

Все ускорения сравнивают исходный узловой временной шаг двойной точности с AMS в одинарной точности.

Результаты, связанные с автомобилестроением

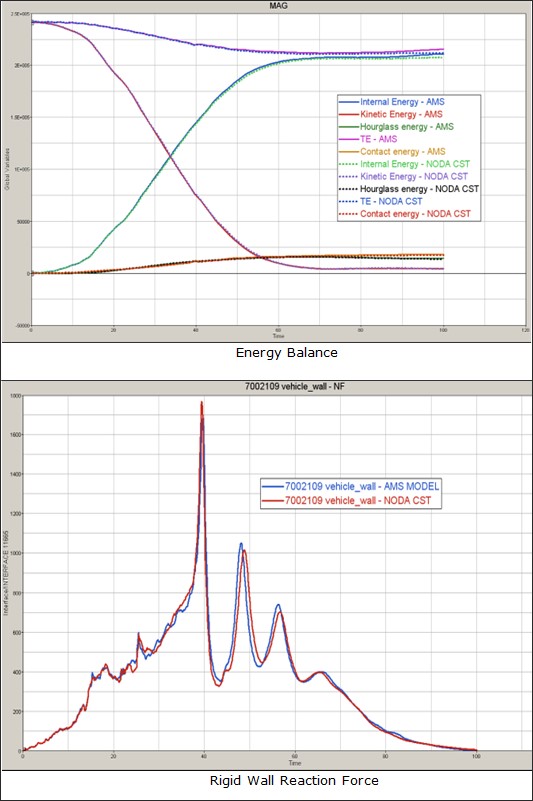
Рисунок 7: OEM1 полностью спереди

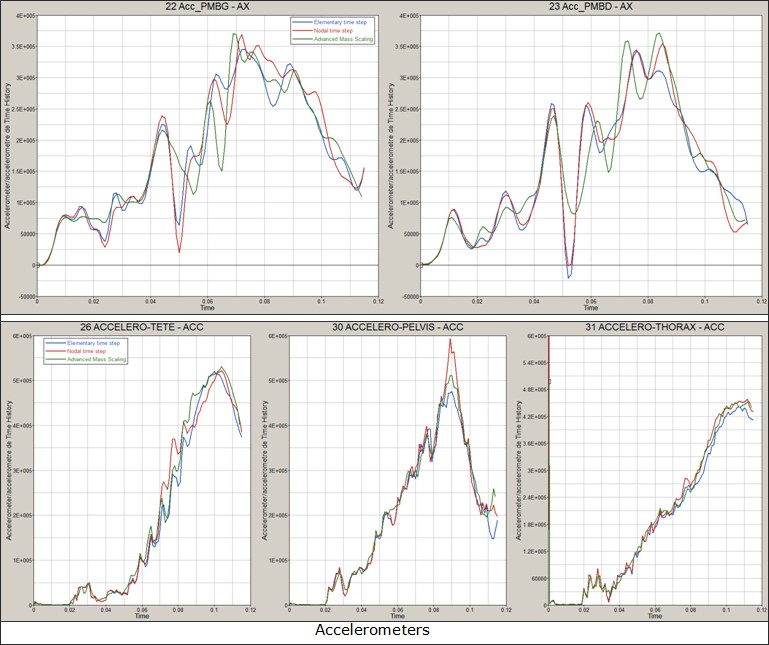
Рисунок 8: Фронтальное смещение OEM2

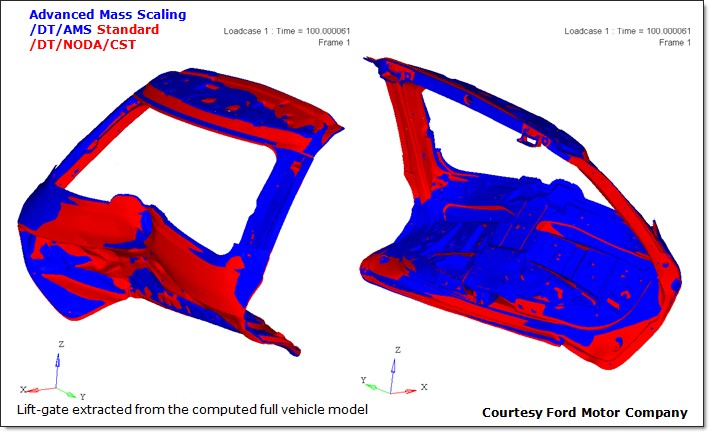
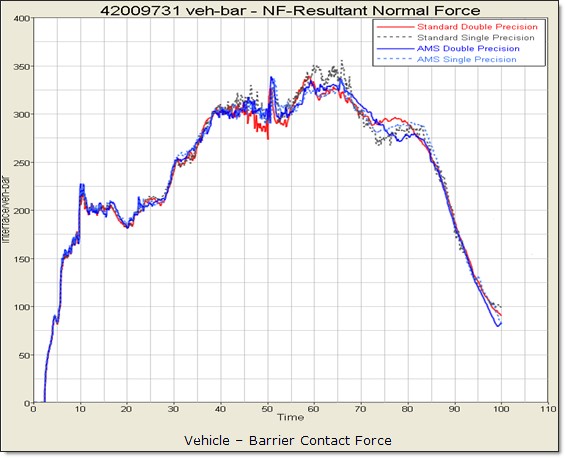
Рисунок 9: Удар спереди и сзади

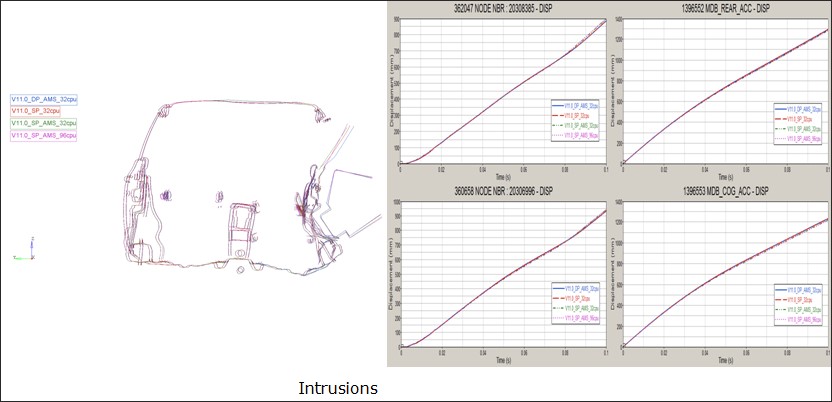
Рисунок 10: Боковой удар OEM4

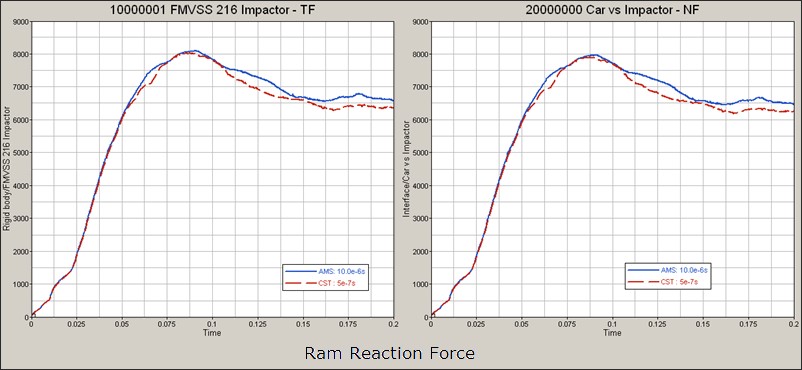
Рисунок 11: Разрушение крыши OEM4

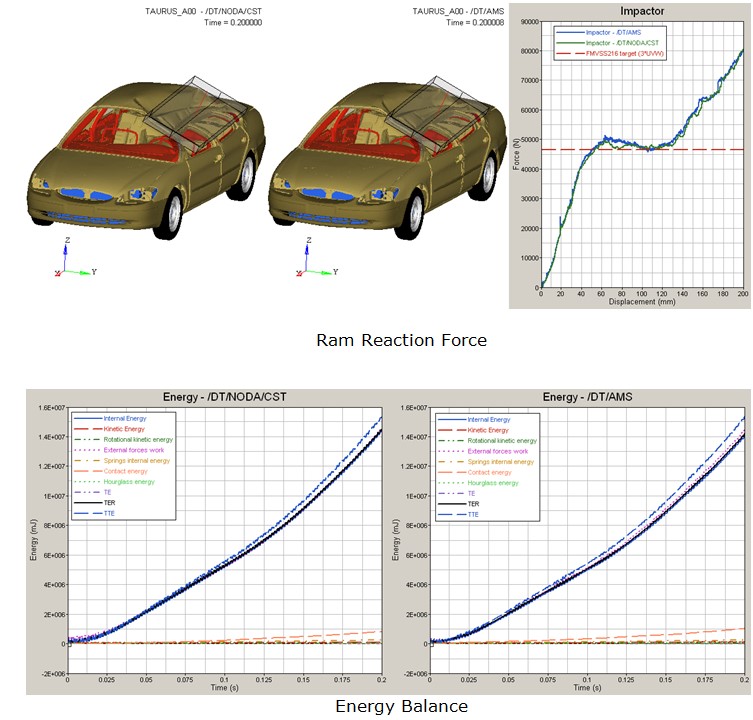
Рисунок 12. Разрушение крыши автомобиля Ford Taurus

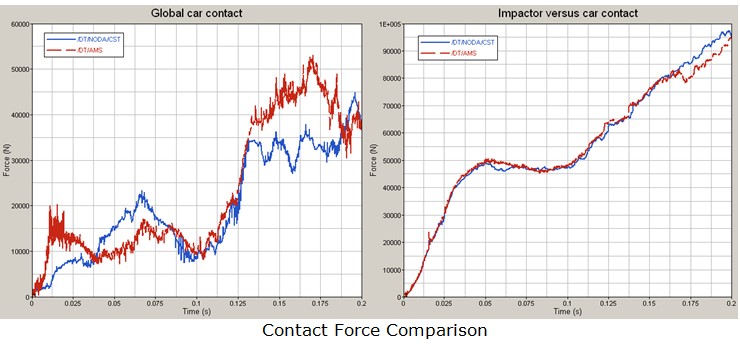
Рисунок 13:

Все ускорения сравнивают исходный узловой шаг времени с AMS с двойной точностью. Серые строки относятся к моделям, которые не запускались повторно в версии 13.0. а ускорения относятся к таблице 4.

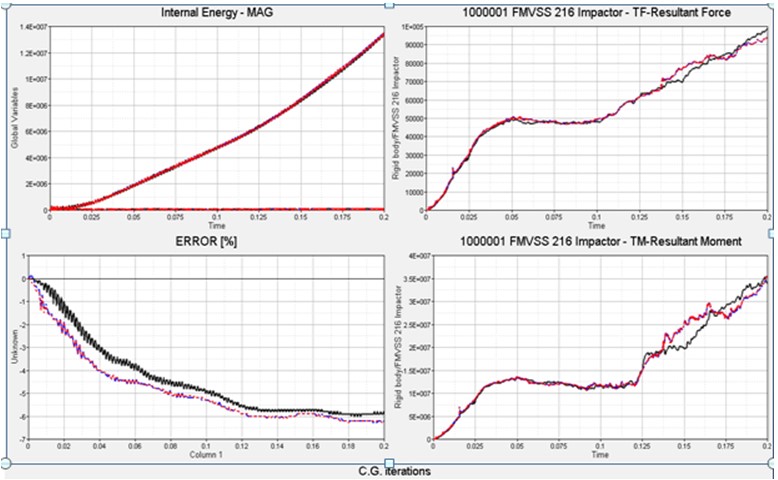
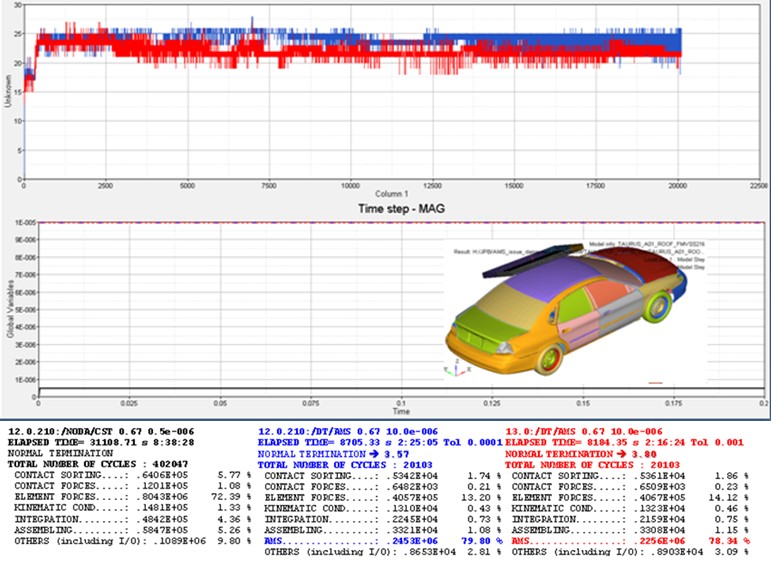
Рисунок 14: повреждение на крыше Ford Taurus

Смотрите также
`/AMS (Starter)`_
`/DT/AMS (Engine)`_

Пример применения обработки металлов давлением

Для обработки металлов давлением и квазистатических нагрузок AMS позволяет получить решение гораздо быстрее и сохранить высокий уровень точности (конечно, используя правильный целевой масштабный коэффициент для временного шага).

Например, для моделирования штамповки обычно масштабный коэффициент 20 обеспечивает точные и очень близкие к эталонным результаты.

Другие методы моделирования обработки металлов давлением, используемые для ускорения решения:

Адаптивность сетки
Динамическая конденсация

По сравнению с адаптивной сеткой, AMS большую часть времени работает быстрее и всегда точнее, чем использование опции адаптивной сетки (/ADMESH).

Однако адаптивность теперь совместима с AMS. Чтобы использовать адаптивную сетку и AMS вместе, необходимо отключить динамическую конденсацию.

Примечание:

AMS может использоваться с более чем двумя уровнями адаптивности. Однако масштабный коэффициент 20 может оказаться слишком высоким в зависимости от количества уровней адаптивности. Эту опцию следует использовать осторожно.

При использовании HyperForm нет необходимости вносить изменения в модель, поскольку оптимизированные параметры AMS заранее определяются автоматически.

Смотрите также
`/AMS (Starter)`_
`/DT/AMS (Engine)`_

1.out примеры файлов

Ниже показано, для одной и той же модели, рассчитанной с помощью PRADIOS версии 11.0.201, эволюция выходного файла Engine (_0001.out) от верифицированного к заниженному наложенному временному шагу AMS.

Смотрите также
`/AMS (Starter)`_
`/DT/AMS (Engine)`_

Завышенный целевой временной шаг /DT/AMS

В 20 раз больше эталона /DT/NODA/CST

Обратите внимание на постепенное переключение с шага времени, управляемого элементом («SOLID»), на шаг времени интерфейса («INTER»), который в конечном итоге заканчивается расхождением AMS.

CYCLE TIME TIME-STEP ELEMENT ERROR I-ENERGY K-ENERGY T K-ENERGY R EXT-WORK
 MAS.ERR
0.000 0.3980E-02 SOLID 1026400 0.0% 0.000 0.4134E+06 0.000 -0.1719E-10
7671E-02
   ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECT_MAXA001 WRITTEN
0.3980E-01 0.3980E-02 SOLID 1026953 0.0% -4.176 0.4134E+06 0.2174 22.59
7671E-02
0.7960E-01 0.3980E-02 SOLID 1027171 0.0% 8.901 0.4135E+06 0.7490 81.41
7671E-02
0.1194   0.3980E-02   SOLID 1027865 0.0% 43.57 0.4135E+06 1.742 164.1
7671E-02
0.1592   0.3980E-02   SOLID 1026669 0.0% 94.41 0.4136E+06 4.155 261.0
7671E-02
0.1990   0.3980E-02   SOLID 1026928 0.0% 158.0 0.4136E+06 9.559 364.5
7671E-02
0.2388   0.3980E-02   SOLID 1027135 0.0% 230.8 0.4136E+06 17.50 470.2
7671E-02
0.2786   0.3980E-02   SOLID 1027670 0.0% 303.5 0.4137E+06 27.21 574.8
7671E-02
0.3184   0.3980E-02   SOLID 1027755 0.0% 366.8 0.4137E+06 36.79 674.5
7671E-02
0.3582   0.3980E-02   SOLID 1027323 0.0% 419.8 0.4137E+06 42.80 767.0
7671E-02
0.3980  0.3980E-02   SOLID 1026690 0.0% 464.3 0.4137E+06 46.51 850.7
7671E-02
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

CYCLE TIME TIME-STEP ELEMENT ERROR I-ENERGY K-ENERGY T K-ENERGY R EXT-WORK
  MAS.ERR
4.378 0.3980E-02 SOLID 1027754 0.0% 2558. 0.4116E+06 61.59 1016.
7671E-02
4.418 0.3980E-02 SOLID 1027894 0.0% 2617. 0.4116E+06 63.80 1002.
7671E-02
4.457 0.3980E-02 SOLID 1026231 0.0% 2680. 0.4115E+06 63.67 990.5
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004937
4.497 0.3980E-02 SOLID 1027738 0.0% 2744. 0.4114E+06 61.73 980.9
7671E-02
4.537 0.3980E-02 SOLID 1027858 -0.1% 2807. 0.4113E+06 59.50 973.5
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004935
4.577 0.3980E-02 SOLID 1027880 -0.1% 2867. 0.4113E+06 58.56 968.7
7671E-02
4.617 0.3980E-02 SOLID 1027278 -0.1% 2926. 0.4112E+06 59.27 966.8
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004933
4.656 0.3980E-02 SOLID 1027327 -0.1% 2984. 0.4111E+06 62.11 968.2
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004931
4.696 0.3916E-02 INTER 42009748 -0.1% 3047. 0.4111E+06 66.28 973.2
7671E-02
4.735 0.3779E-02 INTER 42009748 -0.1% 3111. 0.4110E+06 72.50 982.0
7671E-02
4.772  0.3709E-02 INTER 42009748 -0.1% 3178. 0.4109E+06 80.35 994.9
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004929
4.809  0.3628E-02 INTER 42009748 -0.1% 3247. 0.4109E+06 89.95 1012.
7671E-02
4.845  0.3591E-02 INTER 42009748 -0.1% 3319. 0.4108E+06 98.18 1033.
7671E-02
4.881 0.3659E-02 INTER 42009748 -0.1% 3394.  0.4107E+06 104.3 1060.
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004927
4.917 0.3621E-02 INTER 42009748 -0.1%  3474. 0.4107E+06 108.6 1090.
7671E-02
4.954 0.3656E-02 INTER 42009748 -0.1% 3561. 0.4106E+06 113.7 1124.
7671E-02
4.990 0.3622E-02 INTER 42009748 -0.1% 3656. 0.4105E+06 117.2 1159.
7671E-02
      ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECT_MAXA002 WRITTEN
5.026 0.3631E-02 INTER 42009748 -0.1% 3760. 0.4105E+06 122.4 1194.
7671E-02
5.062 0.3585E-02 INTER 42009748 -0.1% 3865. 0.4104E+06 122.7 1226.
7671E-02
5.098 0.3567E-02 INTER 42009748 -0.1% 3972. 0.4103E+06 125.0 1255.
7671E-02
5.133 0.3578E-02 INTER 42009748 -0.1% 4074. 0.4102E+06 126.3 1280.
7671E-02
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  . . . . . . . . . . .

79.47 0.6686E-03 INTER 42009748 -9.4% 0.2141E+06 0.1554E+06 1465. -4253.
7671E-02
-- RUPTURE OF SHELL ELEMENT NUMBER 873536
-- RUPTURE OF SHELL ELEMENT NUMBER 873327
79.48 0.6686E-03 INTER 42009748 -9.4% 0.2141E+06 0.1554E+06 1465. -4254.
7671E-02
-- RUPTURE OF SHELL ELEMENT NUMBER 873995
79.48 0.6685E-03 INTER 42009748 -9.4% 0.2141E+06 0.1554E+06 1466. -4255.
7671E-02
-- RUPTURE OF SHELL ELEMENT NUMBER 872733
79.49 0.6684E-03 INTER 42009748 -9.4% 0.2141E+06 0.1554E+06 1466. -4256.
7671E-02
-- RUPTURE OF SHELL ELEMENT NUMBER 876109
-- RUPTURE OF SHELL ELEMENT NUMBER 876112
79.50 0.6684E-03 INTER 42009748 -9.4% 0.2141E+06 0.1554E+06 1467. -4257.
7671E-02
-- RUPTURE OF SHELL ELEMENT NUMBER 874081
-- RUPTURE OF SHELL ELEMENT NUMBER 874082
** ERROR : AMS IS LIKELY DIVERGING:
     TOTAL C.G. ITERATION NUMBER = 1000 AT CYCLE NUMBER 39550
79.50 0.6685E-03 INTER 42009748 NaN% 0.2141E+06 NaN NaN -4258.
7671E-02
                      ** CPU USER TIME **

Case: AMSmaxi_ x20 _ div 79.5stop_32cpu_14.5h_ 110201 sep30

Почти приемлемый шаг по времени /DT/AMS

В 13 раз больше эталона /DT/NODA/CST

Обратите внимание на позднее переключение с временного шага, управляемого элементом (SH3N и SOLID), на временной шаг интерфейса (INTER) из-за жесткости их пружинной реакции и управляемого узла (NODE) из-за вращений, тогда как перевод элемента изначально контролировал временной шаг.

(Отклонений AMS нет, задание успешно завершилось на 37220^th цикле в течение 100 мс)

  CYCLE TIME TIME-STEP ELEMENT ERROR I-ENERGY K-ENERGY T K-ENERGY REXT-WORK
   MAS.ERR
0.000 0.2736E-02 SOLID 1026805 0.0% 0.000 0.4134E+06 0.000 .1719E-10
7671E-02
    ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECT_OPT1A001 WRITTEN
0.2736E-01 0.2736E-02 SOLID 1026339 0.0% -9.938 0.4134E+06 0.9492E-01 11.27
7671E-02
0.5472E-01 0.2736E-02 SH_3N 980467 0.05% -2.140 0.4135E+06 0.2769 41.40
7671E-02
0.8209E-01 0.2736E-02 SH_3N 983904 0.0% 12.94 0.4135E+06 0.7553 86.61
7671E-02
0.1094 0.2736E-02 SOLID 1025858 0.0% 34.57 0.4135E+06 1.560 142.9
7671E-02
0.1368 0.2736E-02 SOLID 1026994 0.0% 65.14 0.4136E+06 2.777 207.0
7671E-02
0.1642 0.2736E-02 SH_3N 979591 0.0% 102.8 0.4136E+06 4.844 276.2
7671E-02
0.1915 0.2736E-02 SH_3N 1011870 0.0% 147.1 0.4136E+06 8.051 348.0
7671E-02
0.2189 0.2736E-02 SOLID 1027827 0.0% 197.0 0.4136E+06 12.51 421.2
7671E-02
0.2463 0.2736E-02 SOLID 1025763 0.0% 249.5 0.4136E+06 17.97 494.7
7671E-02
0.2736 0.2736E-02 SOLID 1026760 0.0% 300.5 0.4137E+06 24.45 567.3
7671E-02
  . . . . .. . . . . . . .. . . . . . .  . . . . . . . . . .. . . . . . . .. . . . . . .. . . . . . . . . .. . . .

  -- RUPTURE OF SHELL ELEMENT NUMBER 9861056
  CYCLE TIME TIME-STEP ELEMENT ERROR I-ENERGY K-ENERGY T K-ENERGY R EXT-WORK
  MAS.ERR
15.04 0.2736E-02 SH_3N 980451 -1.0% 0.3598E+05 0.3741E+06 377.9 1060.
7671E-02
15.06 0.2736E-02 SH_3N 980451 -1.0% 0.3607E+05 0.3740E+06 379.4 1048.
7671E-02
15.09 0.2736E-02 SH_3N 980440 -1.0% 0.3614E+05 0.3739E+06 380.1 1035.
7671E-02
15.12 0.2736E-02 SH_3N 983880 -1.0% 0.3623E+05 0.3738E+06 379.8 1021.
7671E-02
15.15 0.2736E-02 SH_3N 1012368 -1.0% 0.3630E+05 0.3737E+06 379.0 1005.
7671E-02
15.17 0.2736E-02 SH_3N 980451 -1.0% 0.3638E+05 0.3736E+06 377.9 987.8
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897179
15.20 0.2736E-02 SH_3N 980112 -1.0% 0.3645E+05 0.3735E+06 377.0 969.7
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9896885
15.23 0.2736E-02 SH_3N 1015803 -1.0% 0.3652E+05 0.3734E+06 376.7 950.6
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897148
15.26 0.2736E-02 SH_3N 1012363 -1.0% 0.3659E+05 0.3733E+06 377.0 930.5
7671E-02
15.28 0.2736E-02 SH_3N 1018445 -1.0% 0.3666E+05 0.3732E+06 377.9 909.5
7671E-02
15.31 0.2736E-02 SH_3N 971703 -1.0% 0.3673E+05 0.3731E+06 378.8 887.8
7671E-02
  . . . . . .. . . . . . .. . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

48.77 0.2393E-02 INTER 42009748 -6.2% 0.1561E+06 0.2282E+06 888.8 -2873.
7671E-02
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7001813
48.79 0.2431E-02 INTER 42009748 -6.2% 0.1562E+06 0.2281E+06 889.2 -2873.
7671E-02
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7002310
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7001709
48.82 0.2495E-02 INTER 42009748 -6.2% 0.1563E+06 0.2280E+06 888.3 -2872.
7671E-02
48.84 0.2607E-02 INTER 42009748 -6.2% 0.1564E+06 0.2279E+06 891.0 -2870.
7671E-02
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7001821
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7002666
48.87 0.2668E-02 NODE 10103704 -6.2% 0.1564E+06 0.2278E+06  893.2 -2869.
7671E-02
-- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7002205
48.90 0.2665E-02 NODE 10103704 -6.2% 0.1565E+06 0.2277E+06  896.1 -2867.
7671E-02
48.92 0.2663E-02 NODE 10103704 -6.2% 0.1566E+06 0.2276E+06  897.3 -2865.
7671E-02
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7001710
48.95 0.2614E-02 INTER 42009748 -6.2% 0.1567E+06 0.2275E+06 897.7 -2863.
7671E-02
48.98 0.2599E-02 INTER 42009748 -6.2% 0.1568E+06 0.2274E+06 895.9 -2861.
7671E-02
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7001702
49.00 0.2655E-02 NODE 10103704 -6.2% 0.1568E+06 0.2273E+06  895.6 -2860.
7671E-02
49.03 0.2736E-02 SH_3N 979131 -6.2% 0.1569E+06 0.2272E+06 896.7   -2859.
7671E-02

  . . . . . . . . . . . .  . . . . . . . . . ..  . . ..  . . . . . . . . . . . . . . . . . . . . . . . .

99.69 0.2612E-02 INTER 42009748 -9.4% 0.2150E+06 0.1548E+06 1712. -3241.
7671E-02
99.7 0.2633E-02 INTER 42009748 -9.4% 0.2150E+06 0.1548E+06 1712. -3239.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 872981
99.74 0.2631E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06 1711. -3237.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 876845
99.77 0.2630E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06 1711. -3235.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877165
99.79 0.2627E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1710. -3233.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 872868
99.82 0.2609E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1709. -3231.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877277
  -- RUPTURE OF SHELL ELEMENT NUMBER 877278
99.84 0.2669E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1709. -3229.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877051
99.8 0.2671E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1708. -3227.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 876266
99.90 0.2671E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1706. -3225.
7671E-02
99.92 0.2660E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1705. -3224.
7671E-02
99.95 0.2643E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06 1704. -3223.
7671E-02
99.98 0.2643E-02 INTER 42009748 -9.4% 0.2150E+06  0.1549E+06 1703. -3222.
7671E-02
     ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECT_OPT1A021 WRITTEN
100.0 0.2623E-02 INTER 42009748 -9.4% 0.2150E+06 0.1549E+06  1703. -3221.
7671E-02
     RESTART FILES: DFWDS734_AMS_FULL_REWELD_NOSECT_OPT1_0001_[0001-0004].rst WRITTEN
     ------------
  ** CPU USER TIME **

Случай: AMSopt1_x13_16cpu_26h_110201сентябрь 30 г.

Приемлемый шаг по времени /DT/AMS

В 12,5 раз больше эталонного значения /DT/NODA/CST

Обратите внимание на временной шаг, управляемый по существу элементом (SH3N), с исключительным влиянием временного шага интерфейса (INTER) и отсутствием временного шага, управляемого узлом (NODE).

(Отклонений AMS нет, задание успешно завершилось на 40230^th цикле в течение 100 мс)

     CYCLE TIME TIME-STEP ELEMENT ERROR I-ENERGY K-ENERGY T K-ENERGY R EXT-WORK
      MAS.ERR 0 0.000 0.2487E-02 SH_3N 987177 0.0% 0.000 0.4134E+06  0.000
   -0.1719E-10 0.7671E-02 ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECT_OPTA001 WRITTEN 10
2487E-01 0.2487E-02 SH_3N 1004312 0.0% -11.02 0.4134E+06 0.7503E-01 9.448 0.7671E-02
0.4975E-01 0.2487E-02 SH_3N 994772 0.0% -2.833 0.4135E+06 0.2556 34.67
7671E-02 30 0.7462E-01 0.2487E-02 SH_3N 980477 0.0% 8.087 0.4135E+06 0.5928
10 0.7671E-02 40 0.9950E-01 0.2487E-02 SH_3N 980465 0.0% 25.51 0.4135E+06
253 121.5 0.7671E-02 50 0.1244 0.2487E-02 SH_3N 994783 0.0% 50.64
4135E+06 2.161 177.3 0.7671E-02 60 0.1492 0.2487E-02 SH_3N 983873 0.0%
66 0.4136E+06 3.542 238.2 0.7671E-02 70 0.1741 0.2487E-02 SH_3N
     983929 0.0% 118.5 0.4136E+06 5.751 302.3 0.7671E-02 80 0.1990 0.2487E-02
  SH_3N 980233 0.0% 160.6 0.4136E+06 9.149 368.2 0.7671E-02 90 0.2239
2487E-02 SH_3N 980624 0.0% 206.9 0.4136E+06 13.47 434.9 0.7671E-02 100
2487 0.2487E-02 SH_3N 985772 0.0% 254.8 0.4136E+06 18.63 501.6 0.7671E-02
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

12.39 0.2487E-02 SH_3N 983878 -0.7% 0.2624E+05 0.3855E+06 319.2 1427.
7671E-02 4990 12.41 0.2487E-02 SH_3N 983854 -0.7% 0.2633E+05 0.3854E+06 317.9
0.7671E-02 5000 12.44 0.2487E-02 SH_3N 980375 -0.7% 0.2642E+05 0.3852E+06
3 1416. 0.7671E-02>
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897228
12.46 0.2487E-02 SH_3N 986833 -0.7% 0.2651E+05 0.3851E+06 317.1 1409.
7671E-02
12.49 0.2487E-02 SH_3N 980402 -0.7% 0.2660E+05 0.3850E+06 316.0 1402.
7671E-02
12.51 0.2487E-02 SH_3N 978799 -0.7% 0.2669E+05 0.3849E+06 316.4 1393.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897051
12.54 0.2440E-02 INTER 42009748 -0.7% 0.2679E+05 0.3848E+06 316.3 1384.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897049
12.56 0.2473E-02 INTER 42009748 -0.7% 0.2687E+05 0.3847E+06 316.3 1375.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897202
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897044
12.59 0.2487E-02 SH_3N 985187 -0.7% 0.2696E+05 0.3846E+06  317.1 1364.
7671E-02
12.61 0.2487E-02 SH_3N 983885 -0.7% 0.2705E+05 0.3845E+06 318.2 1353.
7671E-02
12.64 0.2487E-02 SH_3N 980507 -0.7% 0.2713E+05 0.3844E+06 319.4 1342.
7671E-02
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  . . . . . . . .  . . . . . . . . . . . .  . . . . . . . .. . .

99.43 0.2487E-02 SH_3N 983740 -6.5% 0.2268E+06 0.1548E+06 1688. -3544.
7671E-02
99.46 0.2487E-02 SH_3N 981895 -6.5% 0.2268E+06 0.1548E+06 1691. -3540.
7671E-02
99.48 0.2487E-02 SH_3N 984028 -6.5% 0.2268E+06 0.1548E+06 1694. -3536.
7671E-02
99.51 0.2487E-02 SH_3N 982888 -6.5% 0.2268E+06 0.1549E+06 1697. -3532.
7671E-02
99.53 0.2487E-02 SH_3N 993482 -6.5% 0.2268E+06 0.1549E+06 1700. -3528.
7671E-02
99.55 0.2487E-02 SH_3N 1002607 -6.5% 0.2268E+06 0.1549E+06 1703. -3525.
7671E-02
99.58 0.2487E-02 SH_3N 986010 -6.5% 0.2268E+06 0.1549E+06 1706. -3521.
7671E-02
99.60 0.2487E-02 SH_3N 981287 -6.5% 0.2268E+06 0.1549E+06 1708. -3518.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 876247
99.63 0.2487E-02 SH_3N 993747 -6.5% 0.2268E+06 0.1549E+06 1711. -3515.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 876267
99.65 0.2487E-02 SH_3N 969592 -6.5% 0.2268E+06 0.1549E+06 1712. -3512.
7671E-02
99.68 0.2487E-02 SH_3N 985183 -6.5% 0.2268E+06 0.1549E+06 1713. -3510.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 876245
99.70 0.2487E-02 SH_3N 979126 -6.5% 0.2268E+06 0.1549E+06 1710. -3507.
7671E-02
99.73 0.2487E-02 SH_3N 981287 -6.4% 0.2269E+06 0.1549E+06 1705. -3504.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 876374
99.75 0.2487E-02 SH_3N 985787 -6.4% 0.2269E+06 0.1549E+06 1699. -3501.
7671E-02
99.78 0.2487E-02 SH_3N 981843 -6.4% 0.2269E+06 0.1549E+06 1694. -3498.
7671E-02
99.80 0.2487E-02 SH_3N 986153 -6.4% 0.2269E+06 0.1549E+06 1691. -3495.
7671E-02
99.83 0.2487E-02 SH_3N 993115 -6.4% 0.2269E+06 0.1549E+06 1689. -3492.
7671E-02
99.85 0.2487E-02 SH_3N 995959 -6.4% 0.2269E+06 0.1549E+06 1688. -3490.
7671E-02
99.88 0.2487E-02 SH_3N 979140 -6.4% 0.2269E+06 0.1549E+06 1688. -3487.
7671E-02
99.90 0.2487E-02 SH_3N 985244 -6.4% 0.2269E+06 0.1549E+06 1689. -3485.
7671E-02
99.93 0.2487E-02 SH_3N 993949 -6.4% 0.2269E+06 0.1549E+06 1691. -3483.
7671E-02
99.95 0.2487E-02 SH_3N 988714 -6.4% 0.2269E+06 0.1550E+06 1694. -3481.
7671E-02
99.98 0.2487E-02 SH_3N 986153 -6.4% 0.2269E+06 0.1550E+06 1697. -3479.
7671E-02
     ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECT_OPTA021 WRITTEN
100.0 0.2487E-02 SH_3N 980714 -6.4% 0.2269E+06 0.1550E+06 1698. -3477.
7671E-02
     RESTART FILES: DFWDS734_AMS_FULL_REWELD_NOSECT_OPT_0001_[0001-0004].rst WRITTEN
     ----------
  ** CPU USER TIME **

Случай: AMSopt_x12.5_32cpu_17.8h_110201сентябрь 30 г.

Заниженный целевой временной шаг /DT/AMS

В 10 раз больше эталонного значения /DT/NODA/CST

Обратите внимание на шаг времени, управляемый уникальным элементом (SH3N). Нет шага времени, управляемого интерфейсом (INTER) или узлом (NODE) (задание успешно завершилось в цикле 50250^th в течение 100 мс)

  CYCLE TIME TIME-STEP ELEMENT ERROR I-ENERGY K-ENERGY T K-ENERGY R EXT-WORK
   MAS.ERR
0.000 0.1990E-02 SOLID 1026809 0.0% 0.000 0.4134E+06 0.000 -0.1719E-10
7671E-02
     ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECTA001 WRITTEN
0.1990E-01 0.1990E-02 SOLID 1027233 0.0% -12.55 0.4134E+06 0.4509E-01 6.263
7671E-02
0.3980E-01 0.1990E-02 SOLID 1026793 0.0% -3.404 0.4134E+06 0.1923 22.77
7671E-02
0.5970E-01 0.1990E-02 SOLID 1026919 0.0% -0.3391 0.4135E+06 0.3412 48.73
7671E-02
0.7960E-01 0.1990E-02 SOLID 1026987 0.0% 11.02 0.4135E+06 0.7014 82.15
7671E-02
0.9950E-01 0.1990E-02 SOLID 1027291 0.0% 25.55 0.4135E+06 1.259  121.6
7671E-02
0.1194  0.1990E-02 SOLID 1026789 0.0% 45.07 0.4135E+06 1.935 165.8
7671E-02
0.1393  0.1990E-02 SOLID 1026910 0.0% 68.49 0.4136E+06 2.833 213.5
7671E-02
0.1592  0.1990E-02 SOLID 1027497 0.0% 95.78 0.4136E+06 4.219 263.7
7671E-02
0.1791  0.1990E-02 SOLID 1027432 0.0% 126.7 0.4136E+06 6.282 315.5
7671E-02
0.1990 0.1990E-02 SOLID 1027197 0.0% 160.8 0.4136E+06 9.184 368.2
7671E-02
. . . . . .  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

12.38 0.1990E-02 SOLID 1027341 -0.6% 0.2623E+05 0.3856E+06 304.8 1425.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897042
12.40 0.1990E-02 SOLID 1026467 -0.6% 0.2630E+05 0.3856E+06 304.8 1422.
7671E-02
12.42 0.1990E-02 SOLID 1027168 -0.7% 0.2637E+05 0.3855E+06 303.9 1418.
7671E-02
12.44 0.1990E-02 SOLID 1026994 -0.7% 0.2645E+05 0.3854E+06 303.5 1413.
7671E-02
12.46 0.1990E-02 SOLID 1026918 -0.7% 0.2652E+05 0.3853E+06 302.8 1408.
7671E-02
12.48 0.1990E-02 SOLID 1027344 -0.7% 0.2659E+05 0.3852E+06 301.9 1402.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897040
12.50 0.1990E-02 SOLID 1027487 -0.7% 0.2667E+05 0.3851E+06 300.8 1395.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897152
12.52 0.1990E-02 SOLID 1027341 -0.7% 0.2674E+05 0.3850E+06 300.0 1388.
7671E-02
12.54 0.1990E-02 SOLID 1027156 -0.7% 0.2681E+05 0.3849E+06 299.5 1381.
7671E-02
12.56 0.1990E-02 SOLID 1027292 -0.7% 0.2688E+05 0.3849E+06 299.1 1372.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 9897037
12.58 0.1990E-02 SOLID 1026512 -0.7% 0.2696E+05 0.3848E+06 299.1 1364.
7671E-02
  -- CONSTANT TIME STEP FOR SOLID ELEMENT NUMBER 7004883
12.60 0.1990E-02 SOLID 1027473 -0.7% 0.2702E+05 0.3847E+06 299.6 1355.
7671E-02
12.62 0.1990E-02 SOLID 1027340 -0.7% 0.2709E+05 0.3846E+06 300.6 1346.
7671E-02
12.64 0.1990E-02 SOLID 1027345 -0.7% 0.2716E+05 0.3845E+06 301.1 1337.
7671E-02
. . . . . .  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

99.44 0.1990E-02 SOLID 1026732 -7.5% 0.2226E+06 0.1550E+06 1683. -3546.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 878377
99.46 0.1990E-02 SOLID 1027394 -7.5% 0.2226E+06 0.1550E+06 1683. -3543.
7671E-02
99.48 0.1990E-02 SOLID 1026474 -7.5% 0.2226E+06 0.1550E+06 1683. -3541.
7671E-02
99.50 0.1990E-02 SOLID 1026918 -7.5% 0.2226E+06 0.1550E+06 1683. -3538.
7671E-02
99.52 0.1990E-02 SOLID 1026842 -7.5% 0.2226E+06 0.1550E+06 1684. -3536.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877707
99.54 0.1990E-02 SOLID 1026846 -7.5% 0.2226E+06 0.1550E+06 1684. -3533.
7671E-02
99.56 0.1990E-02 SOLID 1026916 -7.5% 0.2226E+06 0.1550E+06 1685. -3531.
7671E-02
99.58 0.1990E-02 SOLID 1026846 -7.5% 0.2226E+06 0.1550E+06 1686. -3529.
7671E-02
99.60 0.1990E-02 SHELL 389951 -7.4% 0.2226E+06 0.1550E+06 1686. -3526.
7671E-02
99.62 0.1990E-02 SOLID 1026916 -7.4% 0.2226E+06 0.1550E+06 1686. -3524.
7671E-02
99.64 0.1990E-02 SOLID 1027698 -7.4% 0.2226E+06 0.1551E+06 1687. -3522.
7671E-02
99.66 0.1990E-02 SHELL 389982 -7.4% 0.2227E+06 0.1551E+06 1687. -3520.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877600
99.68 0.1990E-02 SHELL 390246 -7.4% 0.2227E+06 0.1551E+06 1688. -3518.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 872853
99.70 0.1990E-02 SOLID 1026474 -7.4% 0.2227E+06 0.1551E+06 1688. -3515.
7671E-02
99.72 0.1990E-02 SOLID 1026911 -7.4% 0.2227E+06 0.1551E+06 1689. -3513.
7671E-02
99.74 0.1990E-02 SOLID 1026914 -7.4% 0.2227E+06  0.1551E+06 1689. -3511.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877814
99.76 0.1990E-02 SOLID 1026500 -7.4% 0.2227E+06 0.1551E+06 1690. -3508.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 875485
99.78 0.1990E-02 SOLID 1027163 -7.4% 0.2227E+06 0.1551E+06 1690. -3506.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 880641
99.80 0.1990E-02 SOLID 1026107 -7.4% 0.2227E+06 0.1551E+06 1690. -3504.
7671E-02
99.82 0.1990E-02 SOLID 1027004 -7.4% 0.2227E+06 0.1551E+06 1691. -3501.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877598
99.84 0.1990E-02 SOLID 1026998 -7.4% 0.2227E+06 0.1551E+06 1690. -3499.
7671E-02
99.86 0.1990E-02 SHELL 390073 -7.4% 0.2227E+06 0.1551E+06 1690.  -3497.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877149
99.88 0.1990E-02 SHELL 254450 -7.4% 0.2227E+06 0.1551E+06 1690.  -3495.
7671E-02
99.90 0.1990E-02 SOLID 1026757 -7.4% 0.2227E+06 0.1551E+06 1690. -3493.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 880538
99.92 0.1990E-02 SOLID 1026603 -7.4% 0.2227E+06 0.1551E+06 1690. -3491.
7671E-02
99.94 0.1990E-02 SOLID 1027433 -7.4% 0.2227E+06 0.1551E+06 1690. -3489.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 877599
99.96 0.1990E-02 SOLID 1026799 -7.4% 0.2227E+06 0.1551E+06 1690. -3488.
7671E-02
99.98 0.1990E-02 SOLID 1027571 -7.4% 0.2227E+06 0.1551E+06 1690. -3486.
7671E-02
100.0 0.1990E-02 SOLID 1027536 -7.4% 0.2227E+06 0.1552E+06 1690. -3485.
7671E-02
  -- RUPTURE OF SHELL ELEMENT NUMBER 872739
     ANIMATION FILE: DFWDS734_AMS_FULL_REWELD_NOSECTA021 WRITTEN
  -- RUPTURE OF SHELL ELEMENT NUMBER 872967
     RESTART FILES: DFWDS734_AMS_FULL_REWELD_NOSECT_0001_[0001-0004].rst WRITTEN
     --------------
     ** CPU USER TIME **

Случай: AMSnorm_x10_16cpu_33.7h_110201сен30.

Масштабный коэффициент временного шага

Теоретический стабильный шаг по времени как для элементов, так и для узлов является приблизительным и может измениться в течение следующего приращения времени.

Чтобы сохранить стабильность моделирования и предотвратить расхождения, рассчитанный теоретический стабильный временной шаг умножается на масштабный коэффициент временного шага $\Delta T_{sca}$ . Если параметры управления временным шагом не используются, то минимальный узловой или элементный временной шаг модели, которая печатается в выходных данных Starter, умножается на масштабный коэффициент временного шага, а результат отображается как TIME-STEP в Выходной файл двигателя.

Минимальный временной шаг, указанный в выходных данных стартера:

   SOLID ELEMENTS TIME STEP
   - - - - - - - - - - - - - - - - -
   TIME STEP             ELEMENT NUMBER
2.6322377948203E-04         11021

Временной шаг элемента по умолчанию активирован в файле Engine:

/DT
0.9 0

Шаг времени двигателя тогда:

TIME-STEP = 0.9 \* 2.6322377948203E-04 = 0.2369E-03 |

Что соответствует нулевому циклу выходного файла Engine:

CYCLE    TIME     TIME-STEP    ELEMENT
   0                0.000     0.2369E-03      SOLID

При использовании любого из методов управления временным шагом, например /DT/NODA/CST или /DT/BRICK/CST, управление временным шагом активируется, когда минимальный временной шаг сетки умножается на время, когда масштабный коэффициент временного шага меньше введенного минимального временного шага, $\Delta T_{sca}*\min(\Delta t_{mesh})\leq\Delta T_{\min}$.

Минимальный временной шаг, указанный в выходных данных Starter, составляет:

NODAL TIME STEP (estimation)

TIME STEP NODE NUMBER

6.9475433E-07 10009

Если в файле Engine используется опция постоянного узлового временного шага:

/DT/NODA/CST
0.9 7.0E-07

Начальный шаг времени двигателя:

\[\text{Initial Time Step}=0.9*6.9475433E-07=0.6253E-06 \tag{11}\]

Поскольку этот начальный шаг по времени меньше $\Delta T_{\min}=7.0E-7$, масса добавляется для увеличения теоретического минимального временного шага сетки. Необходимо добавить достаточную массу, чтобы увеличить минимальный временной шаг сетки, чтобы $\Delta T_{sca}*\min(\Delta t_{mesh})\leq\Delta T_{\min}$ , что означает:

\[\min(\Delta t_{mesh})=\frac{\Delta T_{\min}}{\Delta T_{sca}}=\frac{7.0E-07}{ 0.9}=0.7778E-06 \tag{12}\]

Выходные данные двигателя показывают, что временной шаг такой же, как введенный, и имеется ошибка массы (MAS.ERR) из-за добавления массы для увеличения временного шага.

CYCLE   TIME            TIME-STEP     ELEMENT   … MAS.ERR
     0.000           0.7000E-06    NODE      10009 0.2887E-01
     0.7000E-06      0.7000E-06    NODE      10009 0.2887E-01
     0.1400E-06      0.7000E-06    NODE      10009 0.2887E-01

Если $\Delta T_{sca}=0,67$, то необходимо добавить больше массы, чтобы сделать теоретический шаг сетки выше.

\[\min(\Delta t_{mesh})=\frac{\Delta T_{\min}}{\Delta T_{sca}}=\frac{7.0E-07}{0.67}=1.0448E-06 \tag{13}\]

Масштабный коэффициент временного шага по умолчанию, равный 0,9, хорошо работает в большинстве ситуаций; однако в некоторых случаях рекомендуются другие значения. Одним из примеров могут быть модели из вспененных материалов, жесткость которых может резко возрасти, как показано на «Рисунок 15».

Рисунок 15: типичное поведение пены

Это увеличение жесткости приводит к уменьшению критического временного шага модели и может вызвать расхождение, если временной шаг моделирования больше критического временного шага модели. Некоторые распространенные ситуации, когда следует использовать шаг по времени, отличный от 0,9:

Модели, использующие расширенное массовое масштабирование /DT/AMS для увеличения шага по времени: $\Delta T_{sca}=0,67$
Модели с вспененными материалами: $\Delta T_{sca}=0.66$
Модель с одним элементом: $\Delta T_{sca}=0.1$
Модель с двумя конечными элементами: $\Delta T_{sca}=0.2$
Модель с более чем тремя конечными элементами: $\Delta T_{sca}=0.9$
Никогда не используйте масштабный коэффициент больше 1,0.

Общие рекомендации

Каждый метод пошагового управления имеет свои преимущества и ограничения.

Чтобы оценить, применим ли используемый метод к моделированию, следует использовать хорошее инженерное суждение. В случае сомнений моделирование без управления шагом по времени можно сравнить с моделированием с управлением шагом по времени, чтобы убедиться в приемлемости результатов.

Структурное динамическое моделирование

Узловой шаг по времени и массовое масштабирование

Для неравномерных сеток метод узлового шага по времени приведет к немного большему шагу по времени, чем элементарный метод. Это можно активировать с параметрами по умолчанию, используя:

/DT/NODA
0.9 0

Большинство симуляций могут выиграть от добавления небольшого количества массы к узлам с наименьшим временным шагом. Следующая опция активирует узловой шаг времени с добавленной массой для соответствия минимальному введенному шагу времени:

/DT/NODA/CST 0.9

$\Delta T_{\min}$

Процесс нахождения определенного шага по времени, который добавляет разумное количество массы, можно выполнить, запуская модель на короткое время без какого-либо масштабирования массы для определения шага по времени симуляции. Это также хорошее время, чтобы узнать, сколько времени, по оценкам PRADIOS, потребуется на выполнение моделирования. Затем увеличьте введенный минимальный временной шаг и снова запустите модель, чтобы отметить количество добавленной массы. Продолжайте этот процесс до тех пор, пока в начале моделирования не будет добавлено разумное количество. В зависимости от моделирования позже может быть добавлено больше массы, что потребует еще одной модификации введенного минимального шага по времени.

Необходимо использовать хорошее инженерное решение, чтобы определить, какую массу можно добавить к модели, чтобы сократить время выполнения. Добавление слишком большого количества массы может повлиять на физику падения или моделирования удара. Это связано с тем, что моделируемый объект весит больше реальной части. В общем, рекомендуется поддерживать количество добавляемой массы на уровне менее 5%, но в зависимости от конкретного моделирования может быть приемлемо и большее количество.

Контактный интерфейс управления симуляцией

Если контакт имеет минимальный временной шаг в моделировании, в выходных данных механизма отображается INTER и номер контакта, который имеет минимальный временной шаг. Это указывает на то, что шаг по времени был уменьшен, чтобы предотвратить прохождение вторичного узла через основной сегмент за один цикл. Во время моделирования контакт может иногда иметь минимальный временной шаг.

Однако если контакт контролирует временной шаг в течение длительного периода времени, необходимо выяснить следующие возможные причины.

Начальные пересечения в модели
Неправильные проникновения в модель.
Неправильное определение материала, что приводит к слишком мягкой контактной жесткости.
Небольшая толщина контакта или зазор

Другим возможным решением является использование /DT/INTER/DEL для удаления из контакта вторичных узлов, которые вызывают падение временного шага. Обычно это делается путем установки /DT/INTER/DEL $\Delta T_{\min}$ в 10–100 раз меньше, чем $\Delta T_{\min}$, используемого в /DT/NODA/CST.

Переключиться на рецептуру с малым штаммом

Если используется формулировка большой деформации по умолчанию, большая деформация твердого элемента может привести к уменьшению шага по времени. Чтобы этого не произошло, можно использовать /DT/BRICK/CST для переключения на формулировку малой деформации при введенном минимальном временном шаге для элементов, свойство которых использует $I_{smstr}$ = 2 или 12.

Пример: ввод двигателя /DT

Для типичного моделирования использование комбинации следующих команд управления шагом по времени может помочь поддерживать разумный шаг по времени в моделировании.

//DT/NODA/CST
0.9

$\Delta T_{\text{min1}}$

/DT/BRICK/CST
0.9

$\Delta T_{\text{min2}}$

//DT/INTER/DEL
0.9

$\Delta T_{\text{min3}}$

При этом $\Delta T_{\text{min2}}$ в два-четыре раза меньше, чем $\Delta T_{\text{min1}}$ и $\Delta T_{\text{ min3}}$ в десять-сто раз меньше, чем $\Delta T_{\text{min1}}$.

Квазистатическое моделирование

Для квазистатического моделирования можно использовать либо традиционное узловое масштабирование массы, /DT/NODA/CST, либо расширенное массовое масштабирование, /DT/AMS. Если событие происходит медленно, то использование большего масштабирования узловой массы часто не повлияет на результаты. Или использование /DT/AMS по рекомендациям работает хорошо.

Курант, Рихард, Курт Фридрихс и Ганс Леви. «Об уравнениях в частных разностях математической физики». Mathematische Annalen 100 (1928): 32–74.

Конечные элементы

На основании механики сплошной среды трехмерное твердое тело можно отнести к определенной категории. Для твердого тела с размерами R, L и t, где t — толщина, L — рабочее направление, а R — радиус кривизны, запишите:

Если L/t > 20 и R/t > 20: предположения о тонкой оболочке верны (модели Кирхгофа или Миндлина).
Если 10 < L/t < 20 и 10 < R/t < 20: скорлупа средней толщины (модель Миндлина).
Если 4 < L/t < 10 и 4 < R/t < 1: толстая оболочка.
Если L/t < 4 или R/t < 4: твердые вещества

Затем к каждому случаю применяется адаптированная сетка конечных элементов:

Теория оболочек: 2D-сетка средней поверхности.
Толстая оболочка: 3D-сетка с допущением постоянного нормального напряжения.
Твердые тела: 3D-сетка без предположения постоянного нормального напряжения.

В PRADIOS доступны все эти составы. Для данной сетки может быть доступно несколько видов составов на основе:

Количество точек интеграции
Метод обновления стресса
Предположение о большой или малой деформации
Параметры пластичности для сужения и интеграции материального закона
тип элемента и формула песочных часов.

Твердые элементы (/PROP/SOLID)

В PRADIOS доступны твердые шестигранники и тетраэдры с линейными и квадратичными интерполяционными функциями.

Линейные элементы лучше с точки зрения потребления времени и памяти, особенно из-за низкой

количество точек интегрирования и больший шаг по времени ($\Delta t=\frac{L}{c})$:

TETRA4: $L=\alpha\sqrt{\frac{2}{3}}=0,816\alpha$
TETRA10: $L=a\frac{\sqrt{5/2}}{6}=0,264a$
BRICK8: $L=\frac{Объем}{\text{самая большая площадь грани}}$
BRICK20: $L\approx\frac{толщина}{2}$

В Таблице 5 суммированы различия между этими элементами. Для BRICK8 использование формулировки совместного вращения объясняется в Библиотеке элементов Руководства по теории радиосигнала; что позволяет избежать накопления ошибок из-за процесса обновления, особенно когда элементы подвергаются большой деформации сдвига. Формулировка не используется по умолчанию для этого элемента и должна быть активирована вами.

Рисунок 16: Твердые сетки конечных элементов в PRADIOS

Твердые элементы можно дегенерировать, чтобы обойти некоторые проблемы с сеткой. Вырожденные элементы могут быть получены путем слияния узлов на одном ребре (шестиграннике) или подавления среднего узла в TETRA10. Использование вырожденных элементов не рекомендуется, но если их нельзя избежать из-за сложной геометрии, важно соблюдать симметрию элемента, чтобы сохранить однородное распределение массы. Некоторые примеры вырожденных твердых элементов показаны на рисунке 17.

Рисунок 17: Примеры дегенерации твердых элементов

Таблица 5: Твердые элементы

Имя элемента	Номер элемента	Формулировка	Комментарии
`BRICK8`	1x1x1 2x2x2	Штраф за случай 1 IP	Используйте формулу совместного вращения. Избегайте песочных часов TYPE2
`HA8`	from 2x2x2 to 9x9x9	—	Обратите внимание на значение, используемое для флага Icpre.
`HEPH`	1x1x1	Физическая стабилизация
`BRI CK20`	2x2x2 или 3x3x3	—	Слишком высокая стоимость элемента
`TET RA4`	1	—	Блокировка сдвига при большой деформации Элемент низкой точности
`TET RA10`	4	—	Высокая стоимость Хорошая точность без блокировки сдвига

Элементы твердотельной оболочки (/PROP/TSHELL)

Элементы HA8, HEPH и BRICK20 можно преобразовать в элементы с твердой оболочкой, установив постоянным нормальное напряжение по толщине.

Это допущение позволяет получить твердые элементы, подходящие для моделирования толстой оболочки, где можно использовать только один элемент по толщине. В дополнение к этим элементам доступны SHELL16, PA6 и другие элементы с твердой оболочкой.

Рисунок 18: Solid-Shell в сравнении с Solid-Shell

Таблица 6: Твердые элементы

Имя элемента	Количество точек интеграции	Формула «Песочные часы»
`HSEPH`	В плоскости: 1. В толщине: до 9.	Физическая стабилизация
`HA8`	От 2x2x2 до 9x9x9	—
`PA6`	В плоскости: 1. В толщине: до 9.	—
`SHELL16`	В плоскости: 3х3 или 2х2. По толщине: до 9.	—

Элементы с твердой оболочкой, особенно SHELL16, могут быть полезны для моделирования конструкций с толстой оболочкой и массивными стыками (рис. 19). Временной шаг, пропорциональный кратчайшему расстоянию между двумя узлами, может быть небольшим в зависимости от толщины и характеристик материала.

Рисунок 19: Применение элементов Solid-Shell

Элементы оболочки

Элементы оболочки (/PROP/SHELL)

Оболочка определяется изогнутой средней поверхностью и толщиной h, которая должна быть очень маленькой по сравнению с двумя другими размерами. Элемент оболочки является наиболее распространенным элементом; Полная модель автокатастрофы состоит как минимум на 90% из элементов оболочки.

К ним относятся мембранная, изгибная и сдвиговая деформация, а нормальное напряжение по толщине всегда равно нулю.

Рисунок 20: Элемент оболочки

В PRADIOS стандартными элементами оболочки являются пластинчатые элементы Mindlin с поперечной сдвиговой деформацией. Эти элементы более точны, чем стандартный элемент Кирхгофа; который не учитывает деформацию; из-за поперечного сдвига плоскость, ортогональная средней плоскости, остается ортогональной при деформации.

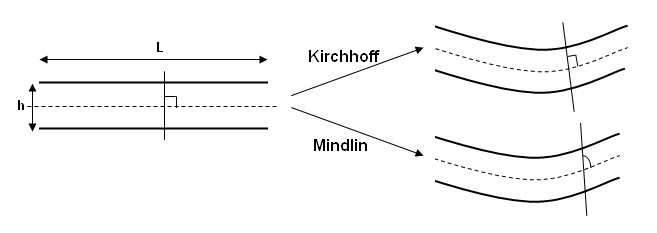
Рисунок 21: Модели корпуса

Даже если модель Кирхгофа менее точна, если отношение L/h больше 20, утверждения Кирхгофа верны; но если отношение L/h находится между 10 и 20, предположение о том, что плоскость, ортогональная средней плоскости, остается ортогональной во время деформации, больше не является действительным, и необходимо рассмотреть модель пластины Миндлина, в которой принимается деформация поперечного сдвига. в учетную запись. В PRADIOS недостаточно интегрированные элементы оболочки (как 4-узловая, так и 3-узловая оболочка) основаны на предположениях Миндлина. Не существует конкретной формулировки, позволяющей смещать среднюю плоскость элемента от узлов; поэтому очень важно дискретизировать конструкции с тонкими стенками на срединной поверхности.

Формулировка элементов оболочки играет значительную роль в моделировании ударопрочности. Элементы оболочки PRADIOS в основном основаны на теории оболочек Миндлина-Рейсснера. Тогда формулировка справедлива как для оболочек средней толщины, так и для тонких оболочек. Неполноценные элементы являются наиболее популярными из-за их низкой стоимости.

Таблица 7: Библиотека элементов оболочки

Элемент	Количество	Формула «Песочные часы»	Комментарии
BT (C lassic Q4)	1	Четыре типа на основе метода штрафов	Постоянный вектор нормали Составы «песочные часы» 3 и 4 типа намного лучше, чем 1 типа – используются по умолчанию.
QEPH	1	Физическая стабилизация Нет выхода в виде песочных часов	Нормальные векторы в узлах с энергией
QBAT	2x2	Полностью интегриров анный элемент	Нормальные векторы в узлах Нет энергии песочных часов
C0	1	—	Плоский фасетный элемент Нет энергии песочных часов
DKT18	3	—	Оболочка Кирхгофа (только тонкая оболочка) Чем выше t/L, тем меньше временной шаг
S3N6	1	—	Оболочка Кирхгофа (только тонкая оболочка) Нет вращательной глубины резкости. Вращение сторон определяется с помощью вертикальных смещений у соседей.

Выбор элемента оболочки для конкретного приложения требует опыта. Следующие общие рекомендации могут оказаться полезными:

Элемент «BT» прост, эффективен и имеет низкую стоимость. Поскольку элемент недостаточно интегрирован, он не очень чувствителен к качеству сетки и может использоваться в случае грубой сетки.
Для случаев квазистатического анализа, мелкой сетки, искривленной поверхности и потери устойчивости рекомендуется использовать элементы QEPH или QBAT.
QBAT — самый точный элемент в PRADIOS. Однако, поскольку он полностью интегрирован, он стоит в два-три раза дороже, чем элемент BT.
«QEPH» — лучший компромисс между стоимостью и качеством. Как правило, он стоит не более 15% от стоимости элемента BT, а результаты, полученные с помощью этого элемента, близки к результатам QBAT.
Треугольники не рекомендуются. Элемент C0 слишком жесткий, а DKT18 стоит дорого. Общее количество треугольников в сетке обычно ограничивается 5% для обеспечения хорошего качества.
Элемент «С3Н6» имеет такие же хорошие характеристики при изгибе, как и «ДКТ18». Его также можно использовать для некоторых специальных приложений, таких как моделирование штамповки.

Связь между качеством результатов и сеткой схематически представлена на рисунке 22.

Рисунок 22: Использование формул оболочки для различных сеток

Интеграция через толщину

В упругой оболочке изменение нормального напряжения по толщине линейно; следовательно, внутреннюю энергию можно получить аналитическим интегрированием. В случае пластичности распределение напряжений становится нелинейным и для учета нелинейности требуется минимум три точки интегрирования. Нелинейное распределение напряжения можно оценить путем измерения значений в некоторых дополнительных точках интегрирования. Качество оценки внутренней энергии зависит от количества точек интеграции и стоимости. Хороший компромисс между стоимостью и качеством можно найти, принимая во внимание нелинейность материала, его толщину и скорость изгиба. В PRADIOS V5x количество точек интеграции можно увеличить до 10. Использование пяти точек интеграции даст лучшие результаты; особенно если толщина превышает 2 мм, но увеличение времени процессора немаловажно. Для имитации мембранного элемента без изгиба и поперечного сдвига достаточно использовать всего одну точку интеграции. Для упругого материала (LAW1) из-за аналитических вычислений опция игнорируется.

Один из способов получить мембранный элемент из эластичного материала – использовать закон упругопластики (закон Джонсона Кука) с очень высоким пределом текучести (пример: 1e+30).

Рисунок 23: Нормальное распределение напряжений в сечении оболочки

Один из способов получить точные результаты с низкими затратами на процессор — использовать глобальную интеграцию. Он заключается в преобразовании критериев пластичности фон Мизеса в так называемые критерии Илюйшина, где компоненты напряжений в точках интегрирования заменяются внутренними силами (N, M, T и т. д.).

Для многослойного элемента оболочки в центре каждого слоя назначается одна точка интеграции.

Примечание: Для композита, состоящего всего из двух слоев, необходимо добавить дополнительные слои (с учетом общей толщины), чтобы получить необходимое количество точек интеграции.

Рисунок 24: Определение слоев для композита для установки количества точек интеграции

Итеративная пластическая проекция

При расчете пластичности должны выполняться два фундаментальных предположения. Во-первых, напряжения в пластической области должны проверяться критериями пластичности (например, критериями Мизеса). Во-вторых, в пространстве главных напряжений есть направление ($\Delta\sigma)$, которое из-за наклепа перпендикулярно поверхности текучести.

По умолчанию к тензору напряжений при проекции на поверхность текучести применяется радиальный возврат. Этот метод лучше, но пластичность приблизительна, и второе предположение не всегда выполняется (рис. 25). Также доступна итеративная ортогональная проекция, этот метод позволяет удовлетворить второму предположению, используя итерационный алгоритм (см. «Элементы оболочки» в Руководстве по теории радиосвязи).

Используйте итеративное проектирование, если требуется высокая точность распределения напряжений после прогнозирования. Это тот случай, когда требуется тензор остаточных напряжений или возвратная пружина. Ошибка радиального возврата выше, когда разница между главными компонентами напряжения велика (например, случай чистого сдвига).

Рисунок 25: Радиальный возврат

Изменение толщины

По умолчанию толщина оболочки предполагается постоянной во время деформации оболочки. Начальная толщина используется для расчета деформаций и интегрирования напряжений, но изменение толщины по-прежнему рассчитывается в целях постобработки. Если используется переменная толщина ($I_thick=1)$, истинная толщина вычисляется не только для последующей обработки, но также для расчета деформации и интегрирования напряжений. ~~~~~~~~~~~

1. Для получения точных результатов, особенно при сужении или пружинении, настоятельно рекомендуется использовать итеративное пластическое проецирование и изменение толщины.

Балочные элементы (/PROP/BEAM, /PROP/INT_BEAM)

Два балочных элемента, доступные в PRADIOS, используются на одномерных конструкциях и каркасах. Она воспринимает осевые нагрузки, поперечные силы, изгибающие и скручивающие моменты (в отличие от фермы, которая воспринимает только осевые нагрузки).

Классическая балка (/PROP/BEAM)

Формулировка по умолчанию основана на формулировке Тимошенко; поэтому учитывается поперечная деформация сдвига. Эта формулировка может выродиться в стандартную формулировку Эйлера-Бернулли, в которой энергия поперечного сдвига не учитывается.

Узлы 1 и 2 используются для определения локальной оси X. Локальная ось Y перпендикулярна оси X и находится в плоскости, определяемой узлами 1, 2 и 3 в момент времени t=0. Затем его положение корректируется на каждом цикле с учетом среднего поворота по оси x. Локальная ось Z получается с использованием правила правой руки.

Рисунок 26: Балочный элемент и локальная система

В PRADIOS геометрия луча определяется площадью его поперечного сечения и тремя моментами инерции площади поперечного сечения. Моменты инерции площади вокруг локальных осей Y и Z относятся к изгибу и могут быть рассчитаны с помощью:

\[I_{y}=\iint_{A}z^{2}dydz \tag{14}\]

\[I_{z}=\iint_{A}y^{2}dydz \tag{15}\]

Момент инерции площади относительно местной оси X соответствует кручению. Его можно просто получить суммированием $I_{y}$ и $I_{z}$. Модель кручения действительна только для полного поперечного сечения, где короблением пренебрегают.

Минимальный шаг по времени для элемента балки определяется с помощью:

\[\Delta t=\sqrt{\frac{aL}{c}} \tag{16}\]

Где,

c

Скорость звука

$\sqrt{E|p}$

$a=\frac{1}{2}\min\biggl{(}\sqrt{\min\biggl{(}4,1+\frac{b}{12}\biggr{)}}\cdot F_{1,}\sqrt{\frac{b}{3}}\cdot F_{2}\biggr{)}$

$F_{1}=\sqrt{1+2d^{2}}-\sqrt{2}\,d$

$F_{2}=\min\biggl{(}F_{1,},\sqrt{1 +2d_{s}2}-\sqrt{2}\,d_{s}\biggr{)}$

$b=\frac{AL^{2}}{\max\biggl{(}I_{y},I_{z}\biggr{)}}$

$d=\max(d_{m,}\,d_{f})$

$d_{s}=d\cdot\max\Biggl{(}1,\sqrt{\frac{12}{b}}\cdot\sqrt{1+\frac{12E}{\frac{5}{6}Gb}(1-I_{shear})}\Biggr{)}$

Вводимыми пользователем параметрами для определения поперечного сечения балки являются три момента инерции площади и площадь. Для обеспечения точности и стабильности рекомендуется соблюдать следующие ограничения:

\[L>\sqrt{A} \tag{17}\]

$0.01A^{2}<I_{y}<100A^{2}$

$0.01A^{2}<I_{z}<100A^{2}$

$0.1\bigl{(}I_{y}+I_{z}\bigr{)}<I_{x}<10\bigl{(}I_{y}+I_{z}\bigr{)}$

Для этого балочного элемента доступны только материалы LAW1 и LAW2. В LAW2 используется глобальная модель пластичности в зависимости от внутренних сил. Основное предположение состоит в том, что поперечное сечение балки полное и прямоугольное. Оптимальное взаимодействие секции и инерции секции:

$12I_{y}I_{z}=A^{4}$

$I_{x}=I_{y}+I_{z}$

Эта модель также дает хорошие результаты для круглого или эллипсоидного сечения. Для тонкостенных сечений глобальная модель пластичности может давать неверные результаты. Не рекомендуется использовать один балочный элемент на одну линию рамной конструкции. Масса собирается в узлы; поэтому для получения правильного распределения массы требуется мелкая сетка. Это особенно актуально, когда важны динамические эффекты.

При этом в лучевом элементе PRADIOS момент не меняется по длине луча. Момент предполагается постоянным и оценивается в центре балки, как и напряжение.

Следовательно, в случае зажатой консольной балки балка будет поддаваться немного большей силе, поскольку момент рассчитывается в центре, а не в основании балки.

Примечание. Выходные данные для балочных элементов выражаются в локальной системе. Некоторые результаты могут сбить с толку из-за того, что локальная система обновляется с учетом среднего вращения (X). Например, для балки с полностью заблокированным одним узлом, если к другому узлу приложить осевую скорость вращения (V), то балка будет вращаться со скоростью (V), но локальная система будет вращаться со скоростью скорость V/2. Это может привести к неправильной интерпретации результатов, особенно поперечных сил и изгибающих моментов.

Новая балка (/prop/int_beam)

Сечение элемента определяется с использованием до 100 точек интегрирования (рис. 27). Свойства элемента поперечного сечения, то есть моменты инерции и площадь, вычисляются PRADIOS как:

\[A = \sum A_{i} = \sum\left({dy_{i}dz_{i}}\right) \tag{18}\]

\[I_{z} = \sum A_{i}(\left\{y_{i}2+\frac{1}{12}dy_{i}2\right) \tag{19}\]

\[I_{y} = \sum A_{i}(\left\{z_{i}2+\frac{1}{12}dz_{i}2\right) \tag{20}\]

Модель балки основана на теории Тимошенко и учитывает деформацию поперечного сдвига без деформации при кручении. Может использоваться для случаев глубоких балок (коротких балок). Использование нескольких точек интегрирования в сечении позволяет получить упругопластическую модель, в которой на каждой точке интегрирования записаны критерии Мизеса и сечение может быть частично пластифицировано в отличие от классического балочного элемента (TYPE3). Также доступен материал LAW36, а также LAW1 и LAW2. Однако, поскольку элемент имеет только одну точку интегрирования по своей длине, не рекомендуется использовать один балочный элемент на линию рамной конструкции, чтобы учесть прогресс пластичности как по длине, так и по глубине.

Рисунок 27: Определения поперечных сечений интегрированной балки

Пружины

Формулировка жесткости

Жесткость пружины можно определить несколькими способами, причем каждая степень свободы определяется по-разному.

Сила и момент

Линейная жесткость и поведение демпфирования

Самая простая формулировка — это линейная упругая пружинная жесткость, где внутренняя сила пропорциональна относительному смещению. В этом случае вводятся только параметр постоянной жесткости $K_{i}$ и дополнительный параметр демпфирования $C_{i}$.

Для линейной жесткости сила и момент равны:

$f(\partial) = K_{i}\partial^{i}$

$M(\theta) = K_{i}\theta^{i}$

Для линейной приборной панели сила и момент равны:

$f(\partial) = C_{i}\partial^{i}$

$M(\theta) = C_{i}\theta^{i}$

Для линейной жесткости и дешпота сила и момент равны:

$f(\partial) = K_{i}\partial^{i} + C_{i}\partial^{i}$

$M(\theta) = K_{i}\theta^{i} + C_{i}\theta^{i}$

Нелинейное поведение

Сила и момент пружины рассчитываются как:

\[\text{F}_{k}\left({\delta^{i}}\right)=\text{f}\left({\frac{{\delta^{i}}}{{\mathit{Ascale}_{i}}}}\right)\left[A_{i}+B_{i}\text{ln}\left({\max\left({1,\frac{{\delta^{i}}}{{\left|{D_{i}}\right|}}}\right)}\right)+E_{i}\left({\frac{{\delta^{i}}}{{\left|{F_{i}}\right|}}}\right)\right\rbrack \tag{21}\]

$+C_{i}{\partial^{i}}+Hscale_{i}\text{ln}\left({\frac{{\delta^{i}}}{{\left({|F_{i}}\right|}}}\right)$

Где $i$ — поступательные степени свободы: 1,2,3.

\[\text{M}_{k}\left({\theta^{i}}\right)=\text{f}\left({\frac{{\theta{i}}}{{\mathit{Ascale}_{i}}}}\right)\left[A_{i}+B_{i}\text{ln}\left({\max\left({1,\frac{{\theta^{i}}}{{\left|{D_{i}}\right|}}}\right)}\right)+E_{i}\left({\frac{{\theta^{i}}}{{\left|{F_{i}}\right|}}}\right)\right. \tag{22}\]

$+C_{i}{\theta^{i}}+Hscale_{i}\text{ln}\left({\frac{{\theta^{i}}}{{\left({|F_{i}}\right|}}}\right)$

Где (i) — вращательные степени свободы: 4,5,6.

Переменные в уравнении силы и момента представляют собой:

$\text{f}\left( {\frac{{\delta^{i}}}{{\mathit{Ascale}_{i}}}} \right)\text{Сила пружины в зависимости от функции смещения, введенная как}\mathit{fct}\_{D_{1i}}$

$\text{f}\left( {\frac{{\theta^{i}}}{{\mathit{Ascale}_{i}}}} \right)\text{Сила пружины в зависимости от функции вращения, введенная как }\mathit{fct}\_{D_{1i}}$

$(A_{i}$, $B_{i}$, $D_{i}$, $E_{i}$ и $F_{i}$\) Коэффициенты масштабирования

$\text{ln}\left( {\max\left( {1,\frac{{\delta^{i}}}{{\left|{D_{i}}\right|}}} \right)} \right)\text{Логарифмическая функция, которая масштабирует жесткость пружины по мере увеличения скорости.}$

Рисунок 28: С вводом параметров

$\text{g}\left( {\frac{{\delta^{i}}}{{\left| {F_{i}} \right|}}} \right)$ Масштабируйте жесткость как функцию линейного входа как $\mathit{fct}\_{D_{2i}}$

$\text{g}\left( {\frac{{\theta^{i}}}{{\left| {F_{i}} \right|}}} \right)$ Масштабируйте момент как функцию входной скорости вращения как $\mathit{fct}\_{D_{2i}}$

Эти входные данные можно использовать для моделирования нелинейных эффектов скорости деформации жесткости пружины.

Рисунок 29: С вводом функции g

$C_{i}$ Линейный коэффициент демпфирования, используемый для увеличения жесткости пружины в зависимости от скорости.

$h\left({\frac{{\delta^{i}}}{{\left|{F_{i}}\right|}}}\right)$ или $h\left ({\frac{{\theta^{i}}}{{\left|{F_{i}}\right|}}}\right)$ Вход функции нелинейного демпфирования как $\mathit{fct}\ _{D_{4i}}$

Линейное или нелинейное демпфирование как функция скорости также можно добавить к силе пружины, используя либо коэффициент линейного демпфирования, либо функцию, определяемую пользователем.

Рисунок 30: С вводом функции h

Обе функции g ang h описывают демпфирующие свойства пружины. Однако функция g масштабирует функцию жесткости пружины f, а функция h добавляет к функции жесткости f.

Шаг времени

Временной шаг для весны:

\[\Delta t=\sqrt{\frac{M}{K}} \tag{23}\]

Временной шаг для Dashpot:

\[\Delta t=\frac{M}{2C} \tag{24}\]

Временной шаг для пружины и приборной панели:

\[\Delta t=\frac{\sqrt{C^{2}+K\cdot M}-C}{K} \tag{25}\]

Где,

$M$ Масса весны

$K$ Линейная жесткость или $\max\Bigl{[}\frac{dF}{d\delta}\Bigr{]}$ для нелинейной пружины

$C$ Линейное демпфирование или $\max\Bigl{[}\frac{\partial\Bigl{(}\frac{d\delta}{dt}\Bigr{)}}{\partial\ Bigl{(}\frac{d\delta}{dt}\Bigr{)}}\Bigr{]}$ для нелинейного демпфирования

Для нелинейных пружин $K$ используется для расчета временного шага и контактной жесткости. Если $K$ не определен в свойстве пружины, максимальный наклон $fct_ID\_{1i}$ $(\max\Bigl{[}\frac{dF}{d\delta }\Bigr{]})$ будет автоматически использоваться для расчета временного шага. То же самое происходит и с демпфирующей жесткостью $C$.

пружинный провал

Выход из строя пружины в объектах TYPE1, TYPE2, TYPE4, TYPE8, TYPE13 и TYPE25 можно рассматривать двумя способами.

однонаправленный отказ, или
Разнонаправленный отказ

Это контролируется опцией $I\_{fail}$. Если флаг $I\_{fail}$ не установлен/не присутствует в свойстве, то для пружины рассматривается однонаправленный сбой по умолчанию. Например, в TYPE4 нет опции $I\_{fail}$, поэтому используется однонаправленный отказ.

Модель разрушения может учитывать разрушение смещения, разрушение силы или разрушение внутренней энергии. Это контролируется опцией $I\_{fail2}$. Подобно $I\_{fail}$, если опция $I\_{fail2}$ не установлена/не присутствует в свойстве, то используется модель отказа смещения (или вращения).

Критерии отказа

Однонаправленный $(I_{fail} = 0)$

Если критерии однонаправленные, пружина выйдет из строя, как только критерии будут удовлетворены для одной степени свободы:

$|\frac{\partial^{i}}{\partial^{i}_{\text{max}}}|\geq 1\text{ or }\left|\frac{\partial^{i}}{\partial^{i}_{\text{min}}}\right|\geq 1\text{ с }\delta^{i}_{\text{max}}\text{ и }\delta^{i}_{\text{min}}\text{ являющийся пределами отказа в направлении }i = 1,2,3.$

$|\frac{\theta^{i}}{\theta^{i}_{\text{max}}}|\geq 1\text{ or }\left|\frac{\theta^{i}}{\theta^{i}_{\text{min}}}\right|\geq 1\text{ с }\theta^{i}_{\text{max}}\text{ и }\theta^{i}_{\text{min}}\text{ являющийся пределами отказа в направлении }i = 4,5,6.$

Где $i$ — любая степень свободы. Его тип свойства зависит.

Для свойства TYPE4 существует только =1 для поступательного X.

Для свойства TYPE8 существуют =1,2,3,4,5,6 для поступательных X, Y, Z и вращательных X,Y,Z.

Для свойства TYPE13 есть =1,2,3,4,5,6, но в данном случае для растяжения/сжатия X, сдвига XY, сдвига XZ, кручения, изгиба Y, изгиба Z.

Примеры поведения при однонаправленном отказе:

Если $\delta^{1}\text{max}=0,04м$ при испытании только на растяжение, то пружина выходит из строя, и сила обращается в ноль, как только удлинение достигает 0,04м. То же самое справедливо и для вращения: если $\theta^{4}\text{max}=0,035рад$ , пружина выходит из строя и имеет нулевую силу при 0,035рад.

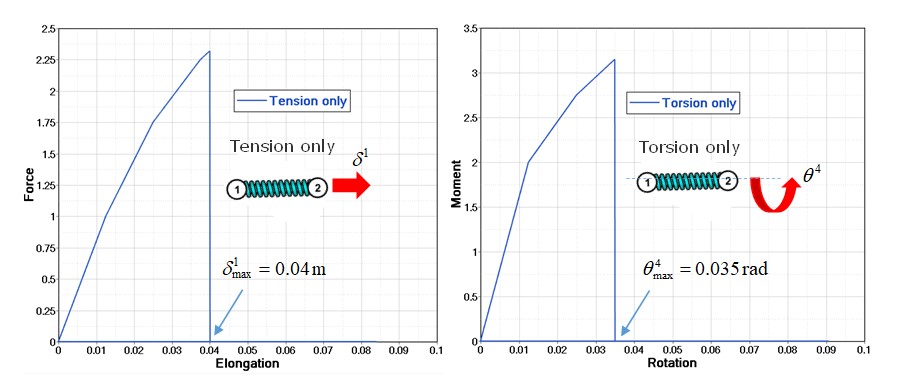
Рисунок 31:

Если на пружину действуют два варианта нагрузки, например, растяжение и кручение и $I_{\text{fail}}=0$ (однонаправленное разрушение), то выход пружины происходит, если любой из них критерий отказа достигнут.

Рисунок 32:

Здесь сначала достигается критерий вращения (при Time=0,58с), затем сила и момент одновременно падают до нуля.

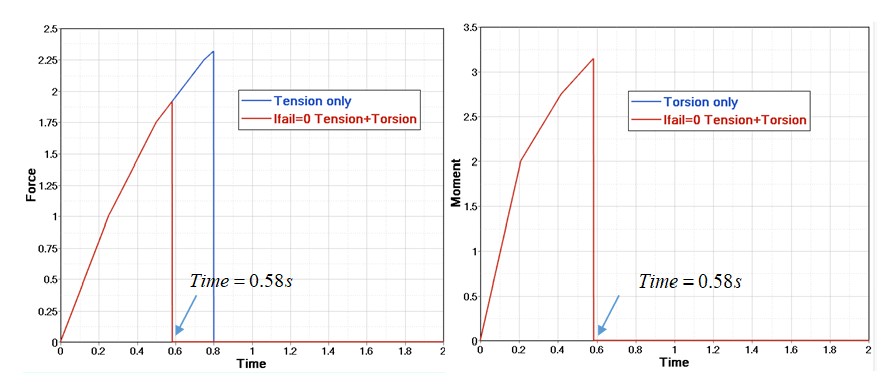
Figure 33:

Многонаправленный $(I_{fail} = 1)$ Если критерии являются многонаправленными, все степени свободы связаны, и сбой происходит, когда:

\[\sum_{i=1,2,3}\alpha^{i}\left(\frac{\delta^{i}}{\delta^{i}_{fail}}\right) ^{\beta^{i}}+\sum_{i=4,5,6}\alpha^{i}\left(\frac{\theta^{i}}{\theta^{i}_{fail }}\right)^{\beta\ {i}}\geq 1 \tag{26}\]

Где $\delta^{i}_{fail}$ и $\theta^{i}_{fail}$ являются критериями отказа. Более подробную информацию см. в разделе «Критерии отказа».

Для свойства TYPE8: $\alpha^{i}=1$ и $\beta^{i}=2$ (критерии отказа показаны синей кривой на рисунке 34).

Для свойств TYPE13 и TYPE25 можно ввести произвольные $\alpha^{i} , \beta^{i}$ с $\alpha^{i}>0$ (по умолчанию $\ альфа^{i}=1$). На рисунке 34 показаны критерии отказа с разными $\beta^{i}$.

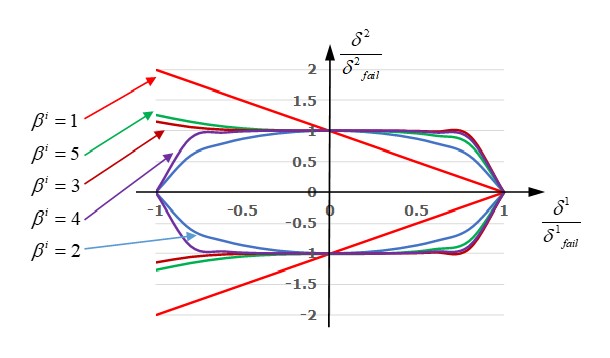
Рисунок 34:

В тестовом примере с двумя вариантами нагрузки растяжение + кручение и с $I_fail = 1.$

Рисунок 35:

При сравнении значения отказа с пределом, установленным только в одном направлении, оно обычно меньше заданного предела. В этом примере предел натяжения установлен на уровне 0,04 м, а предел скручивания — на 0,035 рад. Пружина выходит из строя при удлинении 0,0236 < 0,04 и повороте 0,02826 < 0,035. Это происходит потому, что разрушающая комбинация растяжения и кручения достигает круга разрушения (рис. 36) и; следовательно, пружина вышла из строя (сила и момент упали до нуля).

Рисунок 36:

Модель отказа

Опция $I_{fail2}$ доступна в свойствах TYPE8, TYPE13 и TYPE25.

Критерии отказа смещения (или вращения) ($I_{fail2}=0)$

\[\sum_{i=1,2,3}\left(\frac{\delta^{i}}{\delta^{i}_{fail}}\right)^{2}+\sum_{i=4,5,6}\left(\frac{\theta^{i}}{\theta^{i}_{fail}}\right)^{2}\geq 1 \tag{27}\]

с,

$\delta^{i}_{fail}=\Bigg{\{} \begin{matrix}\delta^{i}_{\max}&if(\delta^{i}>0) \\delta^{i}_{\min},&if(\delta^{i}\leq 0)\end{matrix} и \theta^{i}_{fail}=\Bigg{\{} \begin{matrix}\theta^{i}_{\max}&if(\theta^{i}>0) \\theta^{i}_{\min}&if(\theta^{i}\leq 0)\end{matrix}$

Критерии отказа смещения (или вращения) с учетом эффекта скорости ($I_{fail2}=1)$

Эти критерии разрушения позволят моделировать пределы разрушения, зависящие от скорости, они доступны для смещения, силы и внутренней энергии. Таким образом, поступательное $delta^{i}_{fail}$ и вращательное $theta^{i}_{fail}$ изменяются с учетом скорости, как:

\[\sum_{i=1,2,3}\left(\frac{\delta^{i}}{\delta^{i}_{fail}}\right)^{2}+\sum_{i=4,5,6}\left(\frac{\theta^{i}}{\theta^{i}_{fail}}\right)^{2}\geq 1 \tag{28}\]

$\delta^{i}_{fail}=\Bigg{\{} \begin{matrix}\delta^{i}_{\max}+c_{i}\left|\frac{v^{ i}}{V_{0}^{i}}\right|^{m}&if(\delta^{i}>0) \\delta^{i}_{\min}-c_{i}\left|\frac{v^{i}}{V_{0}^{i}}\right|^{m}&if(\delta^{i}\leq 0)\end{matrix}\ и \theta^{i}_{fail}=\Bigg{\{} \begin{matrix}\theta^{i}_{\max}+c_{i}\left|\frac{v^{ i}}{\omega_{0}^{i}}\right|^{m}&if(\theta^{i}>0) \\theta^{i}_{\min}-c_{i}\left|\frac{v^{i}}{\omega_{0}^{i}}\right|^{m}&if(\theta^{i}\leq 0)\end{matrix}$

Параметр $c_{i}$ представляет собой масштаб экспоненциальной функции, а параметр $ni$ влияет на отказ, как показано на рисунке 37.

Рисунок 37:

Приведенные выше формулы действительны для критериев смещения/вращения, а также являются критериями силы/момента и энергии.

Критерии силы (или момента) ($I_fail2 = 2)$ и критерии внутренней энергии ($I_fail2* = 3)$

Трансляционная $\delta^{i}_{fail}$ и вращательная $\theta^{i}_{fail}$ неудача:

\[\sum_{i=1,2,3}\Biggl{(}\frac{\delta^{i}}{\delta^{i}_{fail}}\Biggr{)}^{2}+\sum_{i=4,5,6}\Biggl{(}\frac{\theta^{i}}{\theta^{i}_{fail}}\Biggr{)}^{2}\geq 1 \tag{29}\]

$\delta^{i}_{fail}=\Bigg{\{} \begin{matrix}\delta^{i}_{max}+c_{i}\left|\frac{v^{i}}{v_{0}}\right|^{ni}, if(\delta^{i}>0) \\ \delta^{i}_{\max}-c_{i}\left|\frac{v^{i}}{v_{0}}\right|^{ni}, if(\delta^{i}\leq 0)\end{matrix} и \theta^{i}_{fail}=\Bigg{\{} \begin{matrix}\theta^{i}_{\max}+c_{i}\left|\frac{\omega^{i}}{\omega_{0}}\right|^{ni}, if(\theta^{i}>0) \\ \theta^{i}_{\min}-c_{i}\left|\frac{\omega^{i}}{\omega_{0}}\right|^{ni}, if(\theta^{i}\leq 0)\end{matrix}$

Приведенные выше формулы действительны для перемещения/вращения, силы/момента и энергии.

Здесь $\delta^{i}_{\max}\delta^{i}_{\min}$ ($\theta^{i}_{\max} , \theta^{i }_{\min})$ не критерий смещения (угла поворота), а максимальная или минимальная сила (момент) для $I_{fail2}=2$ и внутренняя энергия для $I_{fail2}= 3$.

Также учитывается влияние скорости: коэффициент относительной скорости $c_{i}$ относится к силе/моменту ($I_{fail2}=2)$ или к внутренней энергии ($I_{fail2}=3)$.

Весенняя закалка

Варианты упрочнения изотропной, кинематической или несвязанной пружины можно определить с помощью флага упрочнения H. Эти примеры включают только жесткость пружины без учета любого демпфирования.

Линейная упругая пружина, H=0

Линейную пружину можно смоделировать, введя только линейную жесткость как $K_{i}$ и $fct_ID_{1i} = fct_ID_{4i} =0$. Для линейной пружины H всегда равно 0.

Рисунок 38: линейная упругая пружина*

с Ч=0

Нелинейная упругая пружина, H=0

Нелинейная упругая пружина моделируется путем определения кривой зависимости силы от смещения $f_{1}$, где на рисунке 39 она определена в $fct_ID_{1i}$. Поскольку модель упругая, загрузка и разгрузка следуют друг за другом. тот же путь.

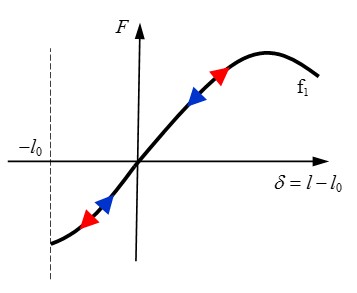
Рисунок 39: Нелинейная упругая пружина*

с Н=0

Нелинейная упругопластическая пружина с изотропным упрочнением, H=1

На рисунке 40 показано поведение нелинейной упругой пластической пружины с изотропным упрочнением, где $f_{1}$ определяется в $fct_ID_{1i}$ и жесткость разгрузки $K_{u}$ является входным значением. используя $K_{i}$.

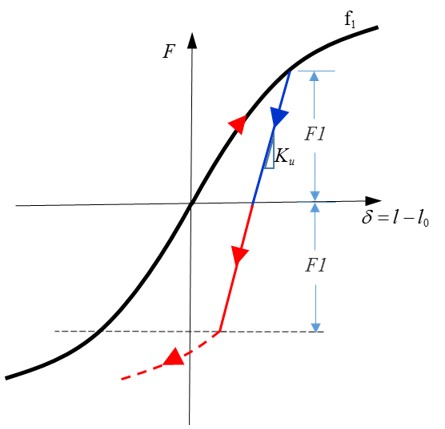
Рисунок 40: Изотропная закалка*

с Н=1

Чтобы продемонстрировать изотропное упрочнение, H=1, на рисунке 41 показана пружина, нагруженная при растяжении, а затем разгружающаяся с использованием линейной жесткости разгрузки, $K_{i}$. Разгрузочная жесткость продолжает использоваться при сжимающей нагрузке до тех пор, пока сила нагрузки при сжатии не совпадет с максимальной силой нагрузки при растяжении. С этого момента любая дополнительная сжимающая нагрузка использует функцию входной нагрузки.

Рисунок 41: Циклическая нагрузка на пружину

с Н=1

Нелинейная упруго-пластическая пружина с несвязанным упрочнением, H=2

Кривая зависимости силы от смещения на рисунке 42 определяется в fct_ID1i, а жесткость при разгрузке вводится с помощью. При использовании несвязанного упрочнения =2 характеристики растяжения и сжатия не связаны. Таким образом, как только разгрузка достигает нулевой силы, жесткость отсутствует до нулевого смещения, и тогда сжимающая нагрузка следует кривой смещения силы.

Рисунок 42: изотропная закалка

с Н=2

Нелинейная упруго-пластическая пружина с кинематическим упрочнением, H=4

Когда используется H=4, функции загрузки $fct_ID_1i$ и выгрузки $fct_ID_3i$ являются миаторными и показаны на рисунке 43 как $f_{1}$ и $f_{3} $ между функцией $f_{1}$ и $f_{3}$ и вводится как $K_{i}$

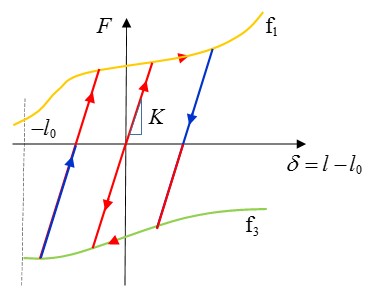
Рисунок 43: кинематическая закалка

с Н=4

Рисунок 44: циклическая нагрузка на пружину

с кинематическое упрочнение H=4

Если кривые минимальной и максимальной текучести ($f_{1}$ и $f_{3}$) имеют одинаковую форму, то упрочнение считается кинематическим.

Рисунок 45: H=4, кривые минимальной и максимальной доходности

($f_{1}$ и $f_{3}$) ввод с одинаковыми фигурами

Нелинейная упруго-пластическая пружина нелинейной разгрузки, H=5

При =5 моделируется несвязанное упрочнение при сжатии и растяжении с нелинейной разгрузкой.

Функция $f_{3}$ определяет остаточное смещение $\delta_{resid}$, связанное со смещением; где разгрузка начинается в $\delta_{peak}$. Разгрузка определяется:

\[F\left(K, f_{3}\right)=a\left(\delta-\delta_{resid}\right)^{n} \tag{30}\]

с, $\delta_{resid}=f_{3}\left(\delta_{peak}\right)$

Где $\alpha\$ вычисляются с использованием $K$ и $f_{3}\left(\delta_{peak}\right)$. Функция нагрузки $f1$ на рисунке 46 определена в $fct_ID_{1i}$, а функция остаточной деформации $f3$ вводится как $fct_ID_{3i}$.

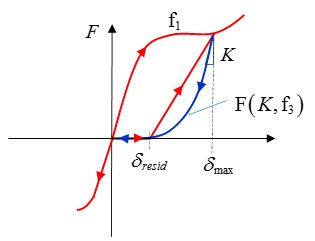
Рисунок 46: Нелинейная разгрузка

с Н=5

На рисунке 47 определена линейная кривая для $\delta_{resid}$ и $\delta_{peak}$ в функции $f_{3.}\delta_{resid}$ в 0,5 раза. $\delta_{peak}$. При циклической загрузке первая выгрузка началась при $\delta_{peak1}$ = 0,05 и $\delta_{resid}$delta_{peak2}` = 0,1 и затем $\delta_{resid}$ = 0,5 * 0,1 = =0,05.

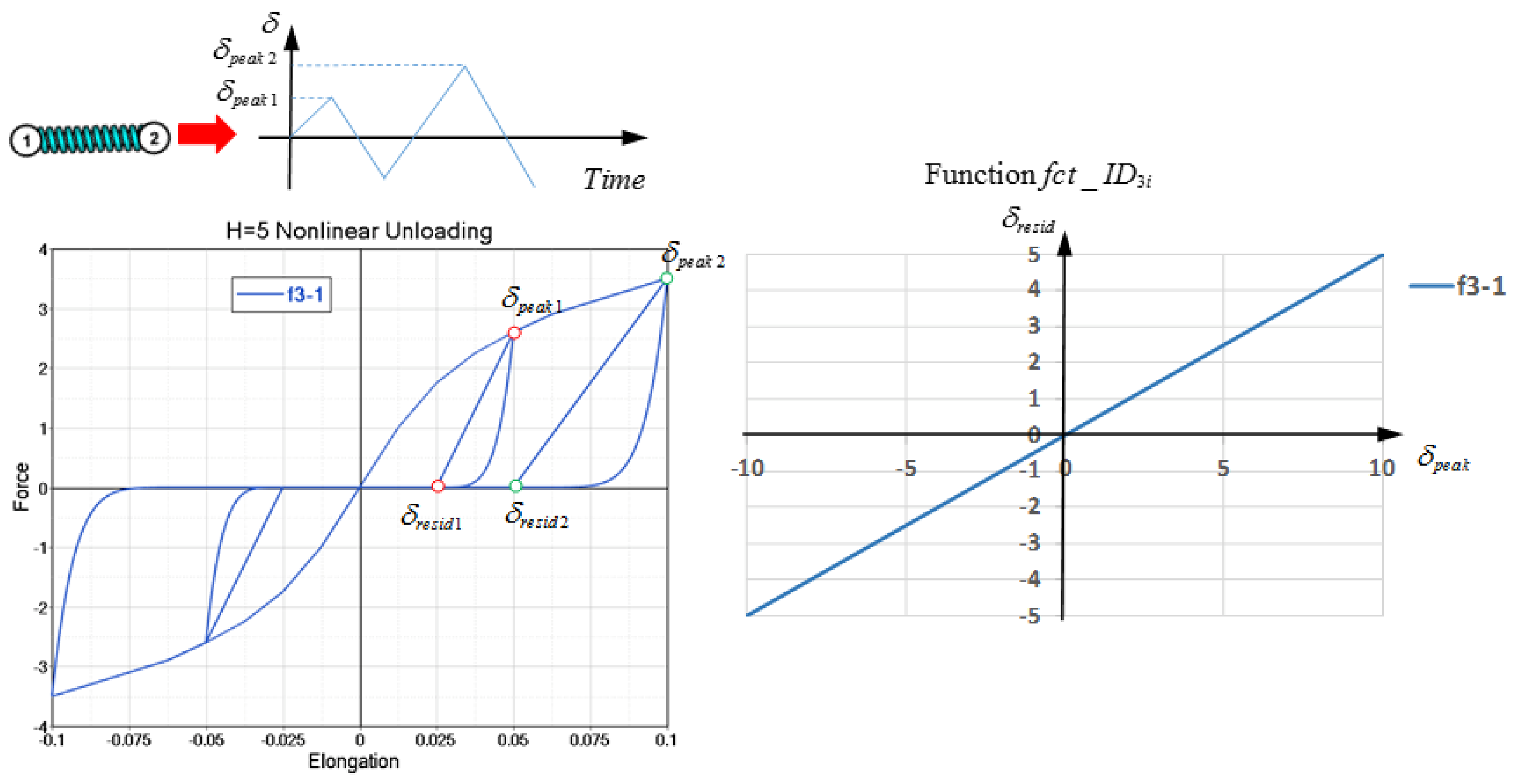
Рисунок 47: Линейная кривая невязки в зависимости от максимального смещения

с Н=5

На рисунке 48 показано, как увеличение наклона кривой остаточного и максимального смещения меняет поведение пружины.

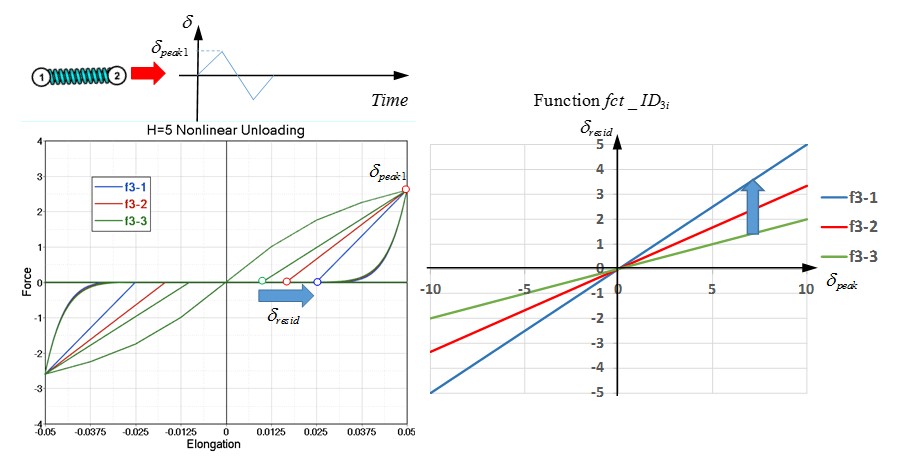
Рисунок 48: Различная кривая линейного остатка и максимального смещения

с Н=5

Сравнивая Рисунок 47 и Рисунок 48, видно, что функция $f_{3}$ влияет только на остаточное смещение $\delta_{resid}$ и форму кривой разгрузки. Форма кривой разгрузки контролируется жесткостью $K$ и $\delta_{peak}$ (смещение начала разгрузки).

Если используются одинаковые жесткости $K$ и одинаковые $\delta_{peak}$, то кривая разгрузки имеет одинаковую форму.

Если используется одинаковая жесткость $K$, но разные $\delta_{peak}$, то кривая разгрузки имеет другую форму.

Если используются разные жесткости $K$ и одинаковые $\delta_{peak}$, то кривая разгрузки имеет другую форму, как показано на рисунке 49.

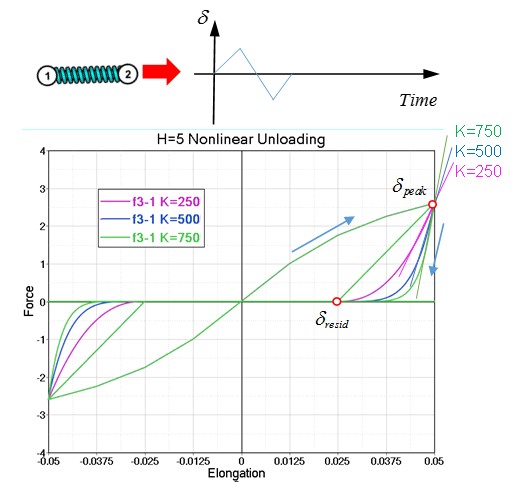
Рисунок 49: Различные значения K

с Н=5

Нелинейная упруго-пластическая пружина, изотропное упрочнение и нелинейная разгрузка, H=6

И H=1, и H=6 представляют собой изотропное упрочнение. В H=6 используется функция нелинейной разгрузки $f_{3}$, а в H=1 используется константа $K_{u}$ для линейной разгрузки. Когда пружина нагружена, а затем разгружена, она следует заданной кривой разгрузки. Кривую разгрузки продолжают использовать при сжимающей нагрузке до тех пор, пока сила нагрузки при сжатии не сравняется с максимальной силой нагрузки при растяжении. С этого момента дополнительная сжимающая нагрузка использует функцию входной нагрузки. Кривая загрузки в $f_{1}$ определяется с помощью $fct_ID_{1i}$, а кривая разгрузки в $f_{3}$ определяется с помощью $fct_ID_{3i}$ .

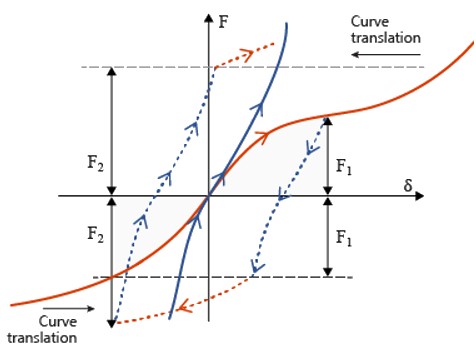
Рисунок 50: Изотропная закалка и нелинейная разгрузка

с Н=6

Нелинейная упруго-пластическая пружина Упругий гистерезис, H=7

с H=7, разгрузка пружины изначально является линейной с использованием входного значения $K$, пока не достигнет кривой разгрузки $f_{3}$. Далее следует дополнительная выгрузка $f_{3}$. Если происходит перезагрузка, жесткость $K$ используется для достижения кривой $f_{1}$, по которой затем следует. Кривая $f_{3}$ должна иметь ординаты меньше, чем кривая $f_{1}$ при определенном значении абсциссы. Кривая загрузки в $f_{1}$ определяется с помощью $fct_ID_{1i}$, а кривая разгрузки в $f_{3}$ определяется с помощью $fct_ID_{3i}$ .

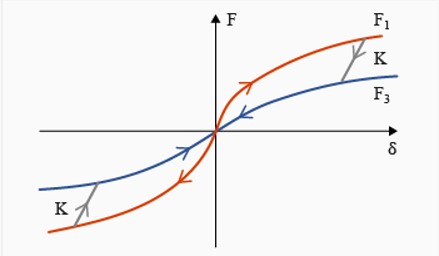
Рисунок 51: Гистерезис упругой нелинейной упругой пластиковой пружины

с Н=7

Пружину с =7 можно использовать для описания поведения гистерезиса. На рисунке 52 показана разница между =0 и =7 при цикловой нагрузке. с =0 (синяя кривая), это нелинейная упругость. Но с =7 (красная кривая), больше энергии (желтая область в первой петле) поглощается из-за петли гистерезиса.

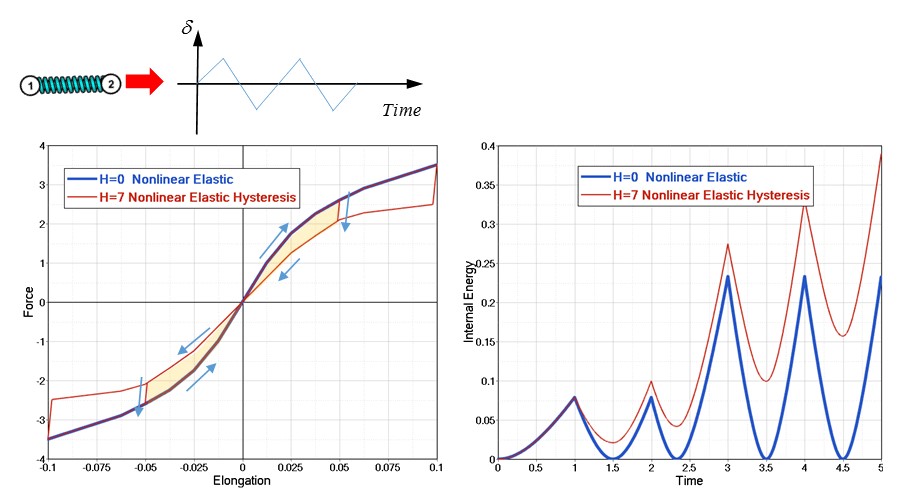
Рисунок 52: Сравнение нелинейной эластики с гистерезисом H=7 и нелинейной эластики H=0

Нелинейная упругая функция общей длины, H=8

Упругая пружина общей длины =8 доступна только в /PROP/TYPE4. В отличие от других вариантов усиления, которые используют изменение длины пружины, эта пружина использует общую длину пружины при определении жесткости пружины. При сжатии жесткость не возникает. Введите $fct_ID_{1i}$, чтобы определить силу в зависимости от общей длины пружины.

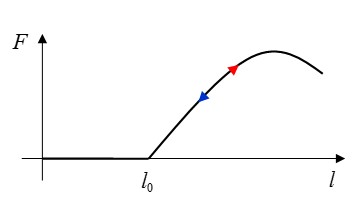
Рисунок 53: Нелинейная упругая функция общей длины

с Н=8

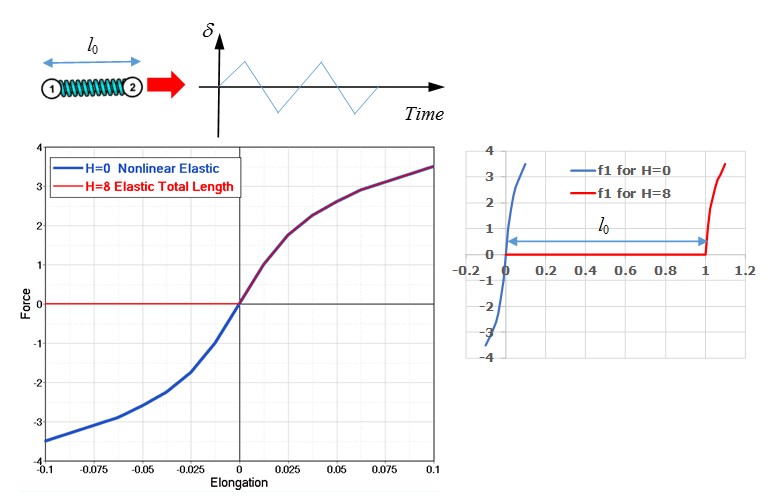
*Рисунок 54: Сравнение H=0 и H=8 при применении циклической нагрузки.

Панель управления

Приборную панель (демпфер) можно смоделировать, не определяя жесткость пружины. Таким образом, после удаления первого члена в уравнении 1 сила становится только функцией постоянного коэффициента демпфирования $C_{i}$ или нелинейной функцией демпфирования силы в зависимости от скорости, как $fct_ID_{4}$.

\[F\big{(}\delta^{j}\big{)}=C_{i}\delta^{j}+Hscale_{j}h\left(\frac{\delta^{j}}{F_{i}}\right) \tag{31}\]

Рисунок 55:

Демпфирование с использованием функции

Помните, что функция $g$ масштабирует силу: $f_{i}\cdot g$, тогда как функция добавляет силу $f_{i}+h$. На рис. 56 сравниваются эти два разных метода.

К нелинейной упругой пластиковой пружине (H=1) прилагается циклическая нагрузка. В двух моделях одна использует функцию g для масштабирования силы, а другая использует функцию h для увеличения силы.

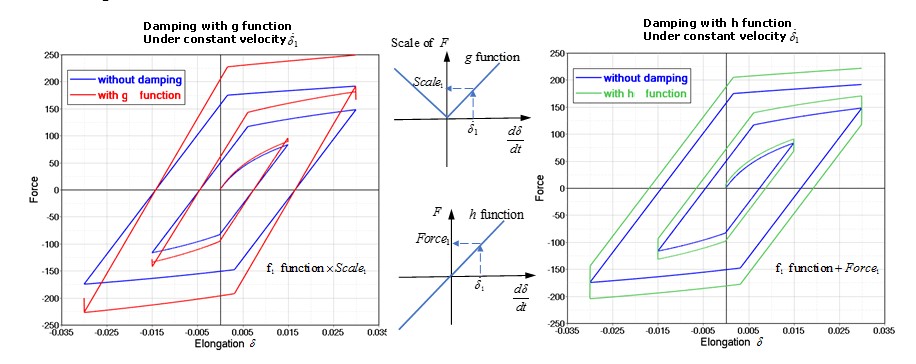
Рисунок 56:

Примечание: Функция должна иметь тот же знак, что и скорость, но функция всегда должна быть положительной, поскольку она является множителем для кривой принудительного смещения $f_{1}$.

Непостоянная жесткость

При создании свойства пружины с помощью определяемой пользователем кривой «Сила в зависимости от смещения» для жесткости, обычно конец кривой имеет очень высокий наклон, чтобы обеспечить очень сильное сжатие. В этом случае часто появляется следующее предупреждение с PRADIOS Starter.

WARNING ID: 506 ** WARNING IN SPRING PROPERTY ** WARNING IN SPRING PROPERTY SET ID=XXX STIFFNESS VALUE 100 IS NOT CONSISTENT с THE MAXIMUM SLOPE (4550) OF THE YIELD FUNCTION ID=X THE STIFFNESS VALUE IS CHANGED TO 1000

This warning comes from the fact that the slope of the input curve (the stiffness) is not consistent с the initial stiffness. If the maximum slope of the curve (the maximum stiffness) is greater than the initial stiffness, unloading in the zone of maximum slope will be false (Figure 1). To obtain proper behavior, PRADIOS Starter modifies the initial stiffness according to the maximum slope.

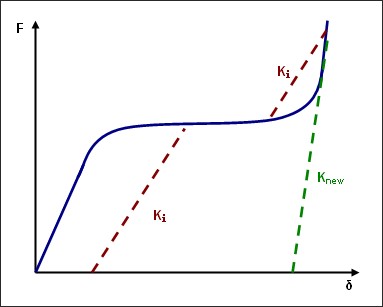
Figure 57: Stiffness not consistent

Spring Coordinate System

Spring Local Coordinate System

Figure 58:

A Spring element is defined using /SPRING с the local coordinate system defined (Figure 58).

Local x direction: from Node N1 to Node N2
Local xy plane: is the plane defined by N1, N2, N3. (N3 optional for 1 DOF springs, if N3 undefined for 3 DOF springs, an appropriate global axis is used).
Local z direction: is normal to the xy plane starting at N1.
Local z direction: y = z /\ y , cross product of the z и x axis.

The type of spring depends on the property assigned to the spring via the /PART.

Spring Coordinate System for Force Computation

Property /PROP/TYPE4 (SPRING), /PROP/TYPE32 (SPR_PRE) и /PROP/TYPE35 (STITCH):

These springs all have one degree of freedom и the force is calculated in the local direction of the spring.
Property /PROP/TYPE8 (SPR_GENE):

Force и moment are calculated either from global system or in user specified skew. The spring has six DOF computed.

◦ If no skew defined then global coordinate system is used

Figure 59: Global coordinate system used in property TYPE8

◦ If skew defined then DOF use skew as,

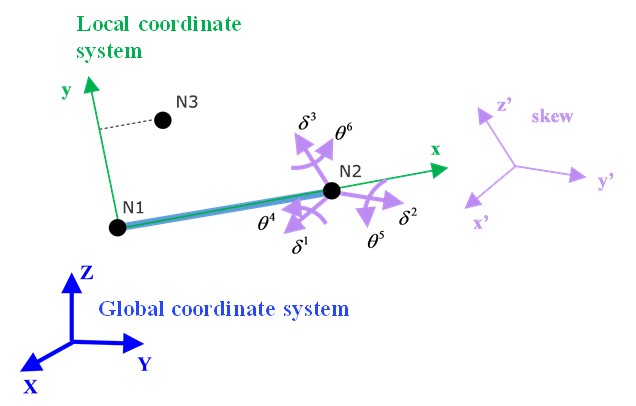
Figure 60: Skew used in property TYPE8

Property /PROP/TYPE13 (SPR_BEAM), /PROP/TYPE25 (SPR_AXI) и /PROP/TYPE44 (SPR_CRUS):

These properites may use either original local system or updated local system с skew or global system. Local x direction is always from Node N1 to N2. Depending on input, z direction may

be determined by Node N3, skew or global system. Finally, y direction is updated so that it is perpendicular to plane xz.

◦ Local x direction: From Node N1 to Node N2.

◦ Local z direction:

∙ If N3 defined, z direction is perpendicular to the plane of N1, N2, N3. These three nodes should not be in a line.

∙ If N3 not defined but skew defined, then z = x /\ y’ с y’ direction from skew.

∙ If N3 и skew are not defined, then с Y direction from global system.

◦ y direction: y direction is computed to be perpendicular to the plane xz, y = x /\ z.

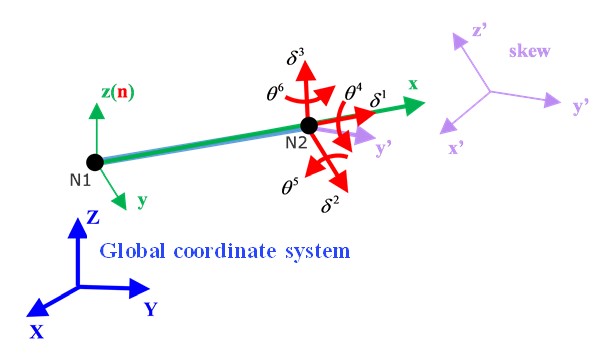
Figure 61: Using skew coordinate system

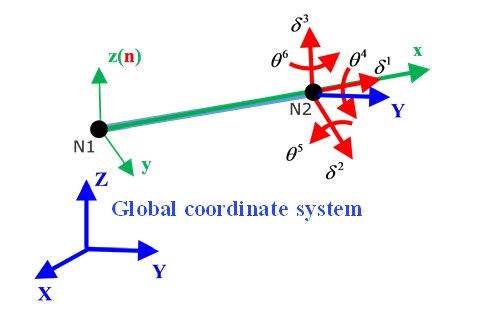
Figure 62: Using global coordinate system

Property /PROP/TYPE45 (KJOINT2):

For each joint type, Node N1 и Node N2 are used to define the joint itself. Node N1 и Node N2 are no longer required to only connect to rigid bodies. Nodes N1, N2 can be non-coincident, but for better behavior of the joints, it is strongly advised to use initially coincident nodes. Optional nodes Node N3, Node N4 are used for the definition of local coordinate systems on two sides of the joint. Initially the coordinate systems are coincident. Behavior of the joint is determined by relative motion/rotation of these local coordinate systems.

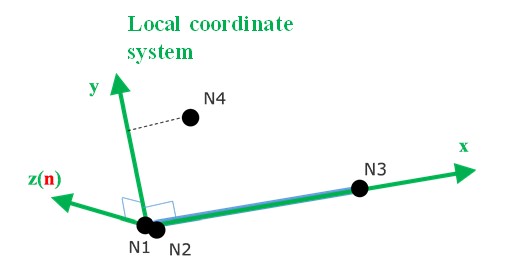
Figure 63:

Nodes of the spherical joints N1, N2 should be preferably coincident. Rigid joints may be described by nodes N1, N2. Global coordinate system is used to define initial orientation of the local coordinate system.

Type No.	Joint Type	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
1	Spherical	x	x	x	0	0	0
8	Regit	x	x	x	x	x	x

x: denotes a fixed degree of freedom

0: denotes a free (user-defined) degree of freedom

Figure 64: Spherical joint

For revolute, cylindrical и translational joints, Node N3 is used to define the first axis of the joint local coordinate system. If N3 is not specified, the axis of the joints is defined using the line between node N1 и N2. In this case, nodes N1 и N2 should not be coincident.

Type No.	Joint Type	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
2	revolute	x	x	x	0	x	x
6	Translational	0	x	x	x	x	x
3	Cylindrical	0	x	x	0	x	x

x: denotes a fixed degree of freedom

0: denotes a free (user-defined) degree of freedom

Figure 65: Spherical joint и Translational joint

Figure 66: Cylindrical joint и Planar joint

For universal, free, и planar joints, nodes N3 и N4 are used to define the first и the second axes of the joint local coordinate system.

Type No.	Joint Type	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
4	Planar	x	0	0	0	x	x
5	Universal (Development source only)	x	x	x	x	0	0
9	Free	x	0	0	0	0	0

x: denotes a fixed degree of freedom

0: denotes a free (user-defined) degree of freedom

Figure 67: Universal joint

When joint properties are non-isotropic (different stiffness, friction or damping for each nonblocked DOF), a full definition of the local coordinate systems is required. In this case the first axis of the local coordinate system is defined by Node N3, the second axis of the local coordinate system is defined by Node N4, и the third axis is computed automatically.

Depending on skew definition, /PROP/TYPE45 (KJOINT2) calculates force и moment.

$Skew\_ID_{1}=0$; $Skew\_ID_{2}=0$ Take spring local coordinate system.

$Skew\_ID_{1}\neq 0$; $Skew\_ID_{2}=0$ Take $Skew\_ID_{1}$

$Skew\_ID_{1}\neq 0$; $Skew\_ID_{2}\neq 0$ Take mean local coordinate system. The x-axis of $Skew\_ID_{1}$ и $Skew\_ID_{2}$ must be parallel.

$Skew\_ID_{1}=0$; $Skew\_ID_{2}\neq 0$ First set global coordinate system in $Skew\_ID_{1}$ Then take mean local coordinate system.

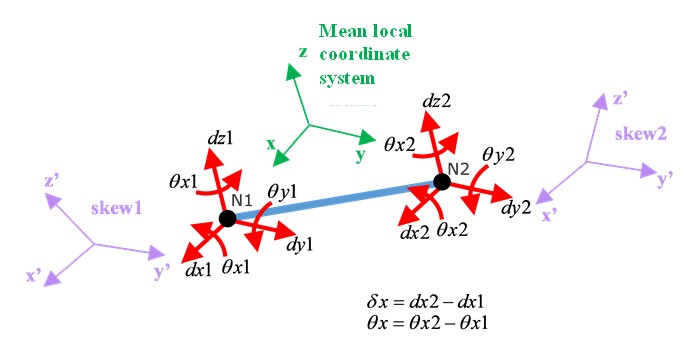
Figure 68: DOF of KJOINT2 properties

See Also
/PROP/TYPE4 (SPRING) (Starter)
/PROP/TYPE8 (SPR_GENE) (Starter)
/PROP/TYPE12 (SPR_PUL) (Starter)
/PROP/TYPE13 (SPR_BEAM) (Starter)
/PROP/TYPE25 (SPR_AXI) (Starter)
/TH/SPRING (Starter)

Spring TYPE4 - 1 DOF Spring (/PROP/SPRING)

Spring TYPE4 is a simple physical spring, physical dashpot or parallel spring и dashpot.

Time step depends on spring mass, stiffness и damping.

Figure 69: Spring TYPE4 - Time Step

Critical spring time step ensures the stability of explicit time integration scheme, but it does not ensure a high accuracy on spring vibration behavior. Only two time steps are available during one vibration period of a free spring. To reproduce the true sinusoidal behavior, reduce the time step by a factor of at least 5. If the spring is used to connect two parts together, the spring vibration period increases и the default spring time step ensures stability и accuracy.

Spring TYPE4 has only one degree of freedom, it can only resist to axial traction и axial compression. The forces applied on the two nodes are always co-linear с local x direction.

Figure 70: Co-linear Forces in Spring TYPE4

If the spring works under compression, it can reach a zero length situation in which the orientation of internal forces can be arbitrary (Figure 71). That can result in stability problems и should be avoided.

Figure 71: Instability of a Zero Length Spring

For further information, refer to the PRADIOS Theory Manual.

General TYPE8 Spring (/PROP/SPR_GENE)

Spring TYPE8 is a six degrees of freedom spring: three translations и three rotations.

Each degree of freedom is independent from the other, и is associated с a specific stiffness (see Stiffness Formulation for more details). To compute the critical time step, the minimum over all degrees of freedom is kept using the following formula:

\[dt = min\left(\sqrt\frac{M}{K}+\sqrt\frac{I}{K_{0}}\right) \tag{32}\]

Where,

$I$ Moment of inertia

$K_{0}$ The related stiffness

The local coordinate system is not associated с the nodes positions, if no local skew is specified (moving or fixed), the global coordinate system is used.

To understи the physical behavior of this mathematical spring, imagine that the two nodes of the spring are chained together. Therefore, only the relative translation/rotation between nodes can be considered as independent degrees of freedom. Figure 72 is a schematic illustration.

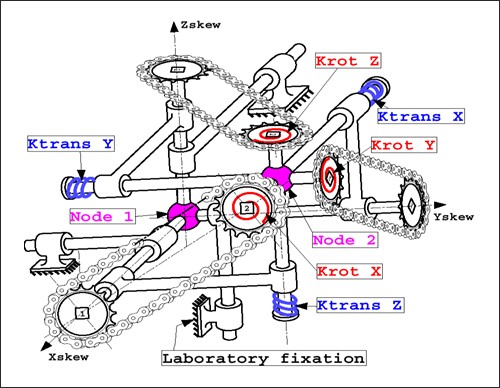
Figure 72: Spring TYPE8

Note: If the local coordinate system is defined through the use of a moving skew, it is possible to emulate the local X-behavior of a spring TYPE4, providing the first two nodes defining the moving skew are node 1 и 2 of the spring (Figure 73).

Figure 73: Deformation in Local X-Direction

It can also be noted that the global force equilibrium is fully respected but not the global moment equilibrium. Therefore, the spring is connected to the laboratory which applies the missing moments. It is generally recommended to use spring TYPE8, only if one node is fixed in all directions or if two nodes are coincident (if the two nodes are coincident, the translational stiffness’ has to be large enough to ensure that the nodes remain near coincident during the simulation). Doing so, the global moment equilibrium is respected.

Note: An increase in energy may be observed if a non-zero length spring TYPE8 undergoes rigid body motion. The spring TYPE8 when their lengths are not zero.

Spring TYPE8 is generally used to model connection between two parts. For example, pivot points in the steering system are modeled с spring TYPE8. To properly model this type of connection, translational degrees of freedom must be blocked through the use of rather high stiffness’ и all rotational degrees of freedom must be set free. Below is an example of such a connection, note that the stiffness values are arbitrary и that they should be adjusted according to a relevant unit system.

Note: It is possible to limit the movement by using a nonlinear stiffness in rotation с a sudden increase (see Stiffness Formulation for mode details).

Figure 74: Modeling of Hinge (Use of Spring TYPE8)

For further information, refer to General Spring Elements (TYPE8) in the PRADIOS Theory Manual.

Spring TYPE12 - Pulley (/PROP/SPR_PUL)

Spring TYPE12 is used to model a pulley. When used in a seat belt model, it is defined с three nodes.

Node 2 is located at the pulley, и a deformable rope is joining the three nodes (Figure 75). The spring mass is distributed on the three nodes с ¼ at node 1 и node 3 и ½ at node 2.

A Coulomb friction can be applied at node 2, taking into account the angle between the two strиs. сout friction, forces are computed as:

\[\left|\mathbf{F}\right|=\left|\mathbf{F}\right|=K\delta \tag{33}\]

с,

:$\delta$ Total rope elongation

:$K$ Stiffness

If the Coulomb friction is used, forces are computed as:

\[\mathbf{F}_{fr}=\min\big{\{}|\Delta\mathbf{F}|,{max}\big{[}0,(|\mathbf{F}|+|\mathbf{F}_{2}|)\cdot\tanh\big{(}\frac{\beta\cdot\mu}{2}\big{)}\big{]}\big{\}}\cdot sig(\Delta\mathbf{F}) \tag{34}\]

Where,

$\mu=\text{f}_{fr}\left(\frac{\Delta F}{Xscale\_F}\right)\cdot Yscale\_F$

$\beta$ Angle (radians unit)

$f_{fr}$ Function of $fcr_ID_{fr}$

$I_{fr} = 0$ (symmetrical behavior)

\[\Delta\mathbf{F}=\left|\mathbf{F}_{1}-\mathbf{F}_{2}\right| \tag{35}\]

$I_{fr} = 1$ (non-symmetrical behavior)

\[\Delta\mathbf{F}=\mathbf{F}_{1}-\mathbf{F}_{2} \tag{36}\]

$\delta_{1}$ is the elongation of strи 1-2 и $\delta_{2}$ of strи 2-3.

Figure 75: Spring TYPE12, Pulley

Time step is computed с the same equation that for spring TYPE4, but the stiffness is replaced с twice the stiffness to ensure stability с high friction coefficients.

Note: The two strиs have to be long enough to avoid node 1, or node 3 slides up to node 2. Nodes 1 и 3 will be stopped at node 2, if there is a knot at nodes 1 и 3.

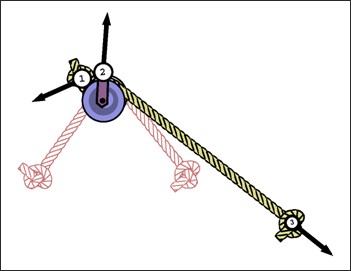
Figure 76: Spring TYPE12, Locking

For further information, refer to the PRADIOS Theory Manual.

Beam TYPE13 Spring (/PROP/SPR_BEAM)

Spring TYPE13 functions like a beam element с several independent modes of deformation:

Traction / Compression
Torsion
Bending (2 modes)
Shear (2 modes)

Contrary to a beam element, relations between displacements (resp. rotations) и forces (resp.

moments) are not deducted from the geometry (area, length, и moment of inertia) и the material properties (Young’s modulus, shear modulus). Instead, they are user-defined through different stiffness formulations (see Stiffness Formulation for more details).

Spring TYPE13 works only if the length is not equal to zero. Nodes 1 и 2 are always used to define the local X-axis. Local Y direction is defined at time t=0 и its position is updated at each cycle, taking into account the mean X rotation. Initially, the Y-axis can be defined in different ways. A third node can be used for beam elements. It is also possible to use the local Y-axis of a skew frame. If a skew frame и third node are not defined, global Y-axis replaces the Y skew axis. If the Y skew axis is co-linear с the local X-axis, the local Y-axis и Z-axis are put in an arbitrary position. The Z-axis is finally computed as the cross product of X-axis и Y-axis.

Figure 77: Spring TYPE13

An illustration of a beam type spring is shown below (Figure 78).

Figure 78: Spring TYPE13

A bending deformation is illustrated in Figure 79. This deformation only takes into account the difference of the two nodes rotations. Beam double bending does generate bending deformation; but shear deformation is shown below.

Figure 79: Spring TYPE13 Under Bending

Figure 80: Spring TYPE13 Under Shear-Bending

The beam type spring behaves as a physical beam, in which the variation of bending moment in length generates the increase in shear. The shear force in the spring implies the change of bending moment.

Note: When defining the spring properties, it is strongly recommended to introduce values с physical meanings. A spring с high shear stiffness и a zero bending stiffness is not recommended и may lead to incorrect results.

Contrary to spring TYPE8, rigid body rotation is possible сout any artificial force и moment generation for spring TYPE13. Behaviors of spring TYPE8 и TYPE13 under a rigid body rotation are compared in Figure 81.

Figure 81: Rigid Body Motions for Spring TYPE8 и TYPE13

To compute the critical time step, the same formula as spring TYPE4 is applied; the minimum overall degree of freedom is finally kept. Therefore to take into account the coupling between bending и shear, и the stiffness’ in bending are modified:

\[K_{yy}\approx K_{yy}+l^{2}K_{z} \tag{37}\]

\[K_{zz}\approx K_{zz}+l^{2}K_{y} \tag{38}\]

Between spring TYPE8 и TYPE13, the sign conventions is not the same, therefore results may be rather confusing when trying to compare both spring. For spring TYPE13, the deformation sign is based on the variation of initial length.

Figure 82: Spring TYPE13 Sign Conventions

For a spring subjected to axial tension, the deformation will always be positive (Figure 82). This is not true any longer for spring TYPE8, since this spring can have a zero length for one (or all) direction, positive и negative spring deformations cannot be defined с the variation of initial length. The sign convention chosen for all degrees of freedom is that a deformation is positive (resp. negative), if displacement (or rotation) of node 2 minus displacement (or rotation) of node 1 is positive (resp. negative).

Figure 83 illustrates the difference between spring TYPE8 и TYPE13, resulting from the sign conventions in PRADIOS.

Figure 83: Difference between Spring TYPE8 и TYPE13

For further information, refer to Beam Type Spring Elements (TYPE13) in the PRADIOS Theory Manual.

Кинематический шарнир TYPE33 (/PROP/KJOINT)

Кинематические шарниры определяются как /PROP/KJOINT. Такие шарниры моделируются при помощи пружины и двух локальных систем координат (SKEW), которые принадлежат связываемым телам.

Предположим, что тела, соединенные шарниром, жесткие, для обеспечения ортогональности осей систем координат, связанных с телами. Однако, можно связывать шарнирами и деформируемые тела. В этом случае, если оси системы координат, связанной с деформируемым телом теряют ортогональность вследствие искажения формы тела, стабильность шарнира обеспечена быть не может.

В PRADIOS существует несколько видов кинематических соединений. Они представлены в таблице ниже.

Type No.	Наименование шарнира	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
1	Сферический	x	x	x	0	0	0
2	Поворотный	x	x	x	0	x	x
3	Цилиндрический	0	x	x	0	x	x
4	Плоскостный	x	0	0	0	x	x
5	Универсальный	x	x	x	x	0	0
6	Переносной	0	x	x	x	x	x
7	Плоскостный без поворотной степени свободы	x	0	0	x	x	x
8	Жесткий	x	x	x	x	x	x
9	Свободный	0	0	0	0	0	0

Здесь: х - заблокированные степени свободы 0 - свободные (заданные пользователем) степени свободы

Свойства шарнира задаются в локальной системе координат (local skew frame), которая определяется при помощи двух систем координат тел, связанных шарниром. Эти системы изначально могут не совпадать. Если начальное положение осей систем координат остается неизменным в течение расчета, то локальная система шарнира определяется в среднем положении. Затем локальная система координат шарнира рассчитывается относительно измененной позиции локальных систем тел.

Всего шесть степеней свободы в шарнире: $\delta X',\delta Y',\delta Z',\theta X',\theta Y',$ и $\theta Z'.$ Все они рассчиты ваются в локальной системе координат шарнира (local skew frame). На рисунке 84 можно видеть схему кинематического шарнира.

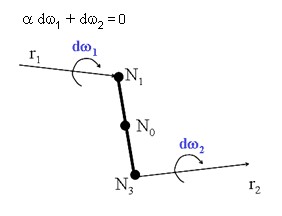
Рисунок 84: Кинематический шарнир

Степени свободы шарниров подразделяются на заблокированные и свободные, т.е незаблокированные. Заблокированные степени свободы имеют постоянную жесткость. Для них рекомендуется выбирать большие значения жесткости относительно жесткости незаблокированных степеней свободы. Пользователь может самостоятельно задавать характеристики жесткости незаблокированным степеням свободы. Они могут быть линейно и нелинейно упругими, а также с вязкостным демпфированием.

Переносные и поворотные степени свободы рассчитываются следующим образом:

\[\delta = dx_{2} - dx_{1}\tag{39}\]

Где, $dx_{1}$ и $dx_{2}$ перемещение двух узлов шарнира в локальной системе координат.

\[\theta = \theta_{2} - \theta_{1}\tag{40}\]

Где, $\theta_{1}$ и $\theta_{2}$ относительные углы поворотов осей двух связанных с телами систем координат, рассчитанных в локальной системе координат шарнира. На рисунке 85 показаны схемы различных кинематических шарниров.

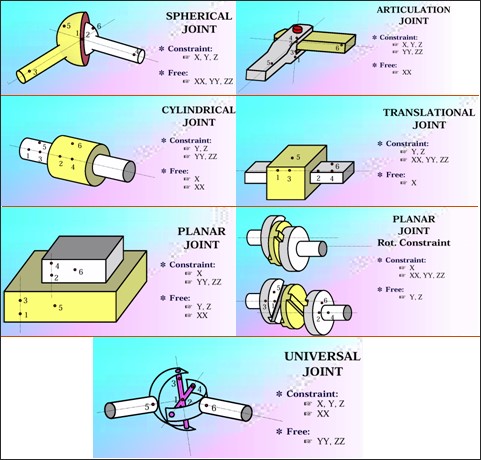
Рисунок 85: Различные кинематические шарниры

Расчет усилий и моментов

Усилия в направлении перемещения δ рассчитываются следующим образом:

Линейная пружина: $\mathbf{F} = \mathbf{K_{t}}\delta + \mathbf{C_{t}\dot\delta}$

$\mathbf{K_{t}}$ : переносная жесткость $(K_{tx}, K_{ty}$ и $K_{tz})$

$\mathbf{C_{t}}$ : переносная вязкость $(C_{tx}, C_{ty}$ и $C_{tz})$

Нелинейная пружина: $\mathbf{F}$ = $\mathbf{K_{t}}f(\delta) + \mathbf{C_{t}}g(\dot\delta)$

Моменты относительно угла поворота $\theta$ рассчитываются следующим образом:

Линейная пружина: $\mathbf{M} = \mathbf{K_{r}\theta} + \mathbf{C_{r}\dot\theta}$

$\mathbf{K_{r}}$ : поворотная жесткость $(K_{rx}, K_{ry}$ и $K_{rz})$

$\mathbf{C_{r}}$ : поворотная вязкость $(C_{rx}, C_{ry}$ и $C_{rz})$

Нелинейная пружина: $\mathbf{M}$ = $\mathbf{K_{r}}f(\theta) + \mathbf{C_{r}}g(\dot\theta)$

Длина шарнира может равняться нулю. Для сферических и универсальных шарниров рекомендуется задавать нулевую длину. Для того, чтобы сохранить баланс моментов в общем случае, в поворотных степенях свободы рассчитываются корректирующие моменты следующим образом:

\[M_{\theta x} = M_{\theta x} + L_{y}\times F_{z} - L_{z}\times F_{y} \tag{41}\]

\[M_{\theta y} = M_{\theta y} + L_{z}\times F_{x} - L_{x}\times F_{z} \tag{42}\]

\[M_{\theta z} = M_{\theta z} + L_{x}\times F_{y} - L_{y}\times F_{x} \tag{43}\]

Поскольку шарниры не имеют массово-инерционных свойств, задаваемых пользователем, в расчетах всегда используется узловой шаг расчета.

Пружинный шарнир TYPE45 (/PROP/KJOINT2)

В PRADIOS property TYPE45 – шарнир пружинного типа.

Степени свободы KJOINT2

Степени свободы KJOINT2 определяются при помощи опции “Type”. Различные типы шар ниров созданы при помощи различных комбинаций степеней свободы.

Таблица 8: Поворотные шарниры.

Type No.	Тип Шарнира	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
1	Сферический	x	x	x	0	0	0
5	Универсальный	x	x	x	x	0	0
2	Вращательный	x	0	0	0	x	x

х - заблокированные степени свободы

0 - свободные (заданные пользователем) степени свободы

Таблица 9: Переносные шарниры

Type No.	Тип Шарнира	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
6	Переносной	0	x	x	x	x	x
6	Oldham	x	0	0	x	x	x

х - заблокированные степени свободы

0 - свободные (заданные пользователем) степени свободы

Таблица 10: Одновременно переносные и поворотные шарниры

Type No.	Тип Шарнира	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
3	Цилиндрический	0	x	x	0	x	x
4	Плоскостный	x	0	0	0	x	x

х - заблокированные степени свободы

0 - свободные (заданные пользователем) степени свободы

Таблица 11: Специальные шарниры

Type No.	Тип Шарнира	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
8	Жёсткий	x	x	x	x	x	x
9	Свободный	0	0	0	0	0	0

х - заблокированные степени свободы

0 - свободные (заданные пользователем) степени свободы

Схемы шарниров показаны на рисунках 86 – 91.

Таблица 12.


Рисунок 86: Сферический	Рисунок 87: Универсальный	Рисунок 88: Поворотный

Таблица 13.


Рисунок 89: Переносной	Рисунок 90: Цилиндрический	Рисунок 91: Плоскостный

Для расчета усилий в пружинах используются координаты степеней свободы. Поэтому для пружины не обязательно задавать локальную систему координат. В зависимости от типа шарнира KJOINT2 и заданной skew, для расчета усилий в пружинах используются различные системы координат.

Жесткость и демпфирование в KJOINT2

В свойствах KJPINT2 используют четыре типа жесткости

Жесткость блокировки Kn. Например:

Если Type = 1 (Сферический), тогда $K_{n}$ блокирующая жесткость для перемещений $d_{x,} d_{y,} d_{z.}$

Если Type = 6 (Переносное), тогда $K_{n}$ тогда Kn блокирующая жесткость для перемещений $d_{y,} d_{z}$ и поворотов $\theta_X,\theta_Y,\theta_Z.$

Таблица 14:

Type No.	Тип Шарнира	dx	dy	dz	$\theta_{x}$	$\theta_{y}$	$\theta_{z}$
1	Сферический	x	x	x	0	0	0
6	Переносной	0	x	x	x	x	x

Если $K_{n}$ = 0 (default), PRADIOS сам рассчитывает жесткость блокировки. Если $K_{n}$ > 0, тогда используется жесткость, заданная пользователем.

Переносная жесткость $K_{ti}$ и поворотная жёсткость $K_{ri}$. Эти жесткости применяются для свободных степеней

свободы и используются для расчета усилий и моментов в шарнирах:

Таблица 15:

Линейная пружина

Нелинейная пружина

$\mathbf{F}$ = $\mathbf{K_{ti}}\delta$

$\mathbf{M}$ = $\mathbf{K_{ri}}\theta$

$K_{ti}$ : переносная жёсткость $(K_{tx,} K_{ty,} K_{tz})$

$K_{ti}$ : поворотная жёсткость $(K_{rx,} K_{ry,} K_{rz})$

Рисунок 92.

$\mathbf{F}$ = $\mathbf{K_{ti}} f (\delta)$

$\mathbf{M}$ = $\mathbf{K_{ri}} f (\theta)$

$K_{ti}$ : фактор переносной жёсткости $(K_{tx,} K_{ty,} K_{tz})$

$K_{ti}$ : фактор поворотной жёсткости $(K_{rx,} K_{ry,} K_{rz})$

$f (\delta)$ функция переносной жёсткости fct_ $K_{ti}$

$f (\theta)$ функция поворотной жесткости fct_ $K_{ti}$

Рисунок 93.

3. Переносной коэффициент вязкости $C_{ti}$ и поворотный коэффициент вязкости $C_{ti}$ для демпфирования. Эти коэффициенты вязкости применяются для свободных степеней свободы и используются для расчета усилий и моментов в шарнирах:

Таблица 16:

Линейная пружина

Нелинейная пружина

$\mathbf{F}$ = $\mathbf{C_{ti}}\dot\delta$

$\mathbf{M}$ = $\mathbf{C_{ri}}\dot\theta$

$C_{ti}$ : переносная жёсткость $(C_{tx,} C_{ty,} C_{tz})$

$C_{ri}$ : поворотная жёсткость $(C_{rx,} C_{ry,} C_{rz})$

$\mathbf{F}$ = $\mathbf{C_{ti}} g (\dot\delta)$

$\mathbf{M}$ = $\mathbf{C_{ti}} g (\dot\theta)$

$C_{ti}$ : фактор переносной жёсткости $(C_{tx,} C_{ty,} C_{tz})$

$C_{ri}$ : фактор поворотной жёсткости $(C_{rx,} C_{ry,} C_{rz})$

$g (\dot\delta)$ функция переносной жёсткости fct_ $C_{ti}$

$g (\dot\theta)$ функция поворотной жёсткости fct_ $C_{ri}$

Например, пружина (которая моделируется KJOINT2) растягивается c постоянной скоростью = 1.33:

Если задана только переносная жесткость равная $K_{t}$ = 100, в этом случае усилие (зеленые кривая на рисунке 94) возрастает на величину $K_{t}$.

Если задана только переносная вязкость равная $C_{t}$ = 50, в этом случает усилие (оранжевая кривая на рисунке 94) будет постоянна, поскольку пружина растягивается с постоянной скоростью. Усилие равно $Force = C_{t}\dot\delta$ = 50 * 1.33 = 66.5.

Если заданы обе – переносная жесткость $K_{t}$ = 100 и переносная вязкость $C_{t}$ = 50 заданы, тогда усилие (синяя линия на рисунке 94) комбинация двух случаев, описанных выше. Усилие равно $Force = K_{t}\delta + C_{t}\dot\delta.$

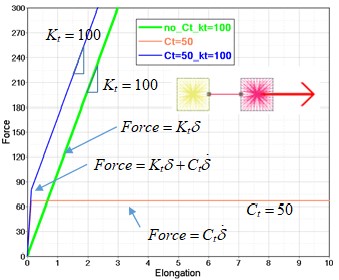
Рисунок 94:

4. Жесткость трения в переносном направлении $K_{f xi}$ и жесткость трения в поворотном направлении $K_{f ri}$. Эти параметры используются для расчета штрафного усилия для того, чтобы перемещение не превысило пределы $SD_{i+,} SD_{i-}$ или угол поворота не превысил пределы $SA_{i+,} SA_{i-}$.

Если $K_{f xi,} K_{f ri}$ не заданы, PRADIOS рассчитает из автоматически с очень большой жесткостью.

Например, рассмотрим тест на растяжение с установленным пределом $SD_{i+}$ = 100, тогда:

Если $K_{f xi}$ не задано (как на рисунке 95 слева), тогда после достижения предела $SD_{i+}$ = 100, генерируется очень высокая жесткость.

Если $K_{f xi}$ = 1000 задано (как на рисунке 95 справа), тогда после достижения предела $SD_{i+}$ = 100 жесткость будет $K_{f xi}$ = 1000.

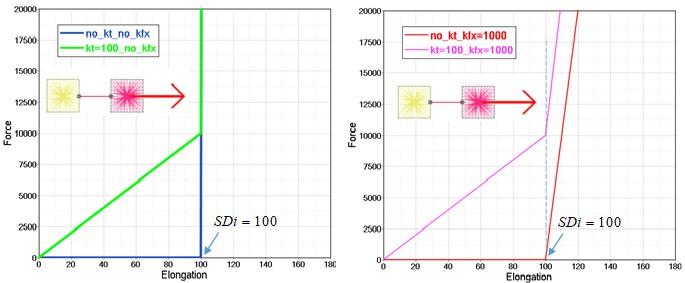
Рисунок 95:

Вышеописанный тест также показывает переносную жесткость $K_{ti}$. Отличие в том, что она влияет на усилие, рассчитываемое в пружине до достижения предела $SD_{i+}$. Значение $Kf_{xi}$ не должно быть очень малым. Это значение используется для моделирования блокировки после достижения предела перемещения. Слишком малое значение $Kf_{xi}$ может привести к сообщению об ошибке:

WARNING ID :         979
\*\* WARNING IN FRICTION DEFINITION FOR KJOINT2
DESCRIPTION :
ELASTIC STIFFNESS 0.1000000000000 IS SMALLER THAN THE MAX DERIVATIVE
720.0000000000 OF THE
FRICTION FUNCTION 0

Если $K_{ti}$ не задан, но задан $K_{f xi}$ = 1000. На рисунке 96 слева показано, как постоянное усилие трения $FF_{i}$ = 15000 влияет на усилие в пружине.

С применением $FF_{i}$ = 15000, усилие увеличивается, т.к. работает жесткость трения $K_{f xi}$ до величины 15000 и затем остается постоянным до достижения предела $SD_{i+}$. После достижения $SD_{i+}$, усилие снова возрастает с жесткостью трения $K_{f xi}$.

Если, как в предыдущем случае, дополнительно задана переносная жесткость $K_{ti}$ = 100 (рисунок 95, справа), тогда усилия возрастают с жесткостью трения

$K_{f xi}$ до $FF_{i} + K_{ti}\delta_{i}$ = 15000 + 100 * 15 = 16500 и затем возрастают с переносной жесткостью $K_{ti}$ = 100 до достижения предела $SD_{i+}$. После достижения $SD_{i+}$, усилия опять возрастают с жесткостью трения $K_{f xi}$.

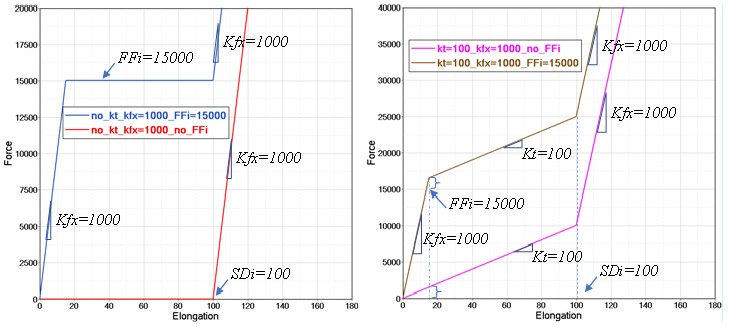
Рисунок 96:

Если нужно описать поведение трения после достижения предела перемещения (поворота),

т.е. после остановки шарнира, необходимо задать жесткости трения $K_{f xi,} K_{f ri}$. В противном случае, даже если было задано постоянное усилие трения $FF_{i,} FM_{i}$ или график изменения усилия трения $fct\_FF_{i,} fct\_FM_{i}$ PRADIOS будет использовать рассчитанную по своим алгоритмам (очень высокую) жесткость для обработки усилий (моментов) после достижения пределов перемещения (поворота) шарнира.

Axisymmetric Spring TYPE25 (/PROP/SPR_AXI)

This spring is a simplification of spring TYPE13; in which the properties of the spring cross-section are considered to be invariable с respect to Y и Z.

That allows you to simplify input formats to avoid errors. For further information about this spring, refer to PRADIOS Starter Input Manual or the PRADIOS Theory Manual.

Mesh Recommendations

Mesh recommendations in crash worthiness и in Implicit Analysis are covered.

Number of Elements Recommended

It is recommended to set a minimum of five to 10 elements in a structural working length. For buckling situation, five to 10 elements along one buckle wave length is also recommended (Figure 97).

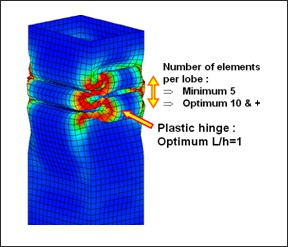
Figure 97: Number of Elements Along a Buckle Wave

On the other hи, due to the direct relation between the size of the smallest element in the mesh и the time step, it is valuable to suppress geometry details, if they are smaller than the average size of elements (Figure 98). A uniform mesh allows you to optimize time step и to ensure the consistency of the momentum transmission during shock wave propagation to avoid parasite reflections. A minimum of three elements along the width is required for better elasto-plastic behavior.

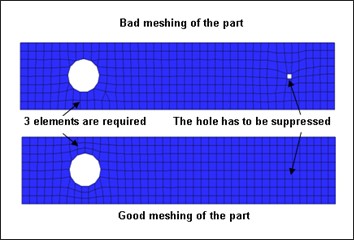
Figure 98: Surface Mesh Generation for Part с Holes

Observe the minimum number of elements, taking into account the mechanical behavior. The minimum number of elements in the width is:

1 for the parts working с quasi-uniform stress distribution as pressure и shear loading сout bending
2 for elastic behavior, including bending
3 for low accuracy elastoplastic behavior
5 for good accuracy elastoplastic behavior
10 for good accuracy elastoplastic behavior, including local loading or local discontinuities

Figure 99: Minimum Number of Elements

Mesh Transition

It is not recommended to use different kinds of element formulation in a given physical part. Fullyintegrated и under-integrated elements do not have the same stiffness matrices; but they do have the same mass matrix. The transition of momentum between these two kinds of elements may be a problem.

To reduce the number of triangles и to improve the consistency of the mesh, the transition patterns illustrated in Figure 100 can be used.

Figure 100: Mesh Transition Examples

Mesh Patterns

с one integration point, there are no element shapes for which the element formulation becomes completely wrong (elements с angles larger than 180 degrees are still working с bad accuracy, but сout numerical problems). It is recommended to use elements as regular as possible с an angle typically between 45 и 120 degrees. The ratio between the largest и smallest edge is not critical for explicit formulation. A uniform mesh is recommended to distribute mass uniformly over the structure. It is possible to avoid triangle creation, even for a triangular geometry or a circle (Figure 101).

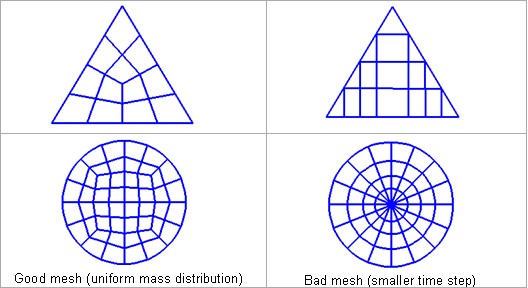
Figure 101: Mesh Transition Examples

In PRADIOS what kind of mesh quality given often depends on the robustness of the elements. Often, an explicit run has different exigencies than an implicit one, for example, homogeneous mesh is more important for explicit (due to time step), than implicit и positive Jacobi warpage, skewness и aspect ratio are more important for implicit (due to convergence), than explicit. Initially, getting a good mesh quality condition is necessary for a good simulation result.

Hourglass Formulations

Under-integrated elements are very familiar in crash worthiness. In these elements, a reduced number of integration points are used to decrease the computation time. This simplification generates zero energy deformation modes, called hourglass modes.

As shown in Figure 102 for an anti-symmetric deformation of a shell element с one integration point at the center, a zero energy mode can be found for a physical deformation mode. That cannot be true from a physical point of view и must be corrected. For a shell mesh, the two main hourglass modes are in-plane (membrane mode) и out-of-plane (W mode).

Figure 102: Zero Energy Mode Generation for a Reduced Integrated Shell

Figure 103: In-plane и Out-of-plane Hourglass Modes

The two correcting methods available are:

Perturbation or penalty method: Hourglass control by application of anti-hourglass forces to maintain deformation stability of the element (historical method).
Physical stabilization method: Hourglass control by the correction of internal energy in an analytical way.

For the first method, four formulations are available in PRADIOS:

Type 1 (Default option): Only in-plane modes are corrected, valid for shells и solids.
Type 2: Old formulation no longer recommended.
Type 3: Plasticity is taken into account in the computation of anti-hourglass forces; in-plane и out-of-plane hourglass modes are corrected; available only for shells.
Type 4: Like Type 1 с additional higher order terms in the computation of anti-hourglass forces и с out-of-plane hourglass mode correction; available only for shells.

The second method is powerful и can be used when the mesh quality is good. The physical stabilization method is incorporated in the following PRADIOS elements:

QEPH shell
HEPH solid
HSEPH solid-shell

The choice of hourglass formulation plays an essential role on the quality of results. If the mesh is fine enough, the physical stabilization method can be used. Otherwise, Type 3 и Type 4 formulations are recommended for shell meshes. When the material undergoes elastic-plastic behavior, the Type 3 formulation is much more efficient. The hourglass coefficient, hm и hf are recommended to be set to 0.1; however, the default value, hf=0.01 can be used for hr.

Stress-Strain Computation Options (/PROP)

Usually a small stress formulation is used to simulate problems for small deformations. Typical application covers linear elastic studies. For nonlinear problems с elasto-plastic behavior и large deformation, it is recommended to use a large strain и large displacement formulation.

For some problems с very large mesh distortion, a large strain formulation has some limitations. If the time step decreases too much, the CPU time will increase highly и if a brick element reaches a negative volume, the computation will stop, or this element may have to be removed.

с a small strain formulation these limitations disappear; however, it seems surprising to use a small strain formulation in case of large deformation; but this can be a better solution than element deletion. For specific materials, like honeycomb, for which there is no Poisson’s effect, the small strain limitation can be corrected just by using the appropriated stress strain curve.

Large Strain Formulation

By default, PRADIOS uses a large strain, large displacement formulation с explicit time integration. By computing the derivative of shape functions at each cycle, large displacement formulation is obtained. The large strain formulation results from incremental strain computation. Stresses и strains are therefore true stresses и true strains.

Time integration of Cauchy stress (true stress) can be performed as:

\[\sigma_{ij}(t + \delta t) = \sigma_{ij} (t) + \frac{d\sigma_{ij}(t)}{dt} dt \tag{44}\]

The objectivity of stress rate means that the stress tensor follows the rigid body rotation of the material. Stress rate is the function of element average rigid body rotation и of strain rate. Stability of explicit scheme is given by Courant condition:

\[\Delta t<\frac{l}{c} \tag{45}\]

с being the element characteristic length и is the sound speed. The time step is computed at each cycle. Large element deformation can provide a large time step decrease. For very large deformations, a negative volume can be reached и then becomes impossible to integrate the stresses over the volume.

Small Strain Formulation

Assuming a constant Jacobian matrix during time и also a constant volume, previous equations degenerate into a small strain formulation. All special variables are then values defined at time t=0 (or at the time the small strain formulation is initiated).

Time step then becomes constant:

\[\Delta t=\frac{l_{0}}{c} \tag{46}\]

Then the effective negative volume has no effect on the computation (only the initial volume is used), but the small strain assumption is acceptable for some specific material behavior, like honeycomb; so the small displacement formulation is obviously not recommended for crash analysis.

For stress objectivity, the Jacobian matrix time transformation depends upon the element deformation и the element rigid body rotation. Rigid body translation has no effect on the Jacobian matrix. If element deformation is not taken into account, a small strain formulation is obtained. If element rigid body rotation is not taken into account, a small displacement formulation is obtained.

To switch to a small strain formulation after reaching $\Delta T_{min}$ , the following options can be used in the Engine file:

/DT/BRICK/CST

$\Delta T_{sca} \Delta T_{min}$

/DT/SHELL/CST

$\Delta T_{sca} \Delta T_{min}$

/DT/SH_3N/CST

$\Delta T_{sca} \Delta T_{min}$

Note: For some brick material laws, the sound speed is pressure dependent. Therefore, it possible that time step becomes slightly smaller than $\Delta T_{min}$.

Update Stress и Strains (/PROP)

In PRADIOS two formulations are available (Figure 104):

Co-rotational Formulation (CR): The FEM equations of each element are referred to two systems. A fixed or base configuration is used to compute the rigid body motion of the element. Then, the deformed current state is referred to the co-rotated configuration, which is obtained by the rigid body motion of the initial reference.
Updated Lagrangian Formulation (ULF): The reference is the last known (accepted) solution. It remains fixed over a step и updated at the end of each step.

Figure 104: Updating Methods in PRADIOS

The co-rotational formulation is the most recent of the formulations in geometrically Nonlinear Structural Analysis. It decouples small strain material nonlinearities from geometric nonlinearities и naturally hиles the question of frame indifference of anisotropic behavior, due to material nonlinearities. For historical PRADIOS solid elements, the co-rotational formulation is optional и should be activated before the computations (refer to /PROP/SOLID).

Note: An updated Lagrangian formulation can hиle incorrect results for solids in large shear deformation, due to the accumulation of updating errors at each cycle. The use of corotational formulation is strongly recommended, especially when elements undergo large shear deformation or large rigid body motions.

PRADIOS Coordinate System

Shell и solid (thick shell) elements are introduced for the coordinate systems.

Global system: ($\mathbf{X}, \mathbf{Y}$ и $\mathbf{Z})$
Natural system (isoparametric frame)
Local element coordinate system ($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$

Figure 105: 4-node shell element

($\mathbf{X}, \mathbf{Y}$ и $\mathbf{Z})$ - Global Cartesian fixed system:

Natural system (non-normalized coordinate system)

is from middle point of Line 14 to middle point of Line 23.
is from middle point of Line 12 to middle point of Line 34.
Plane is in the middle surface of shell element и is normal of the middle surface.

($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$ - Local coordinate system (orthogonal, normalized elemental coordinate system):

$\mathbf{z}$ is normal of middle surface.
($\mathbf{x}$ и $\mathbf{y}$) are in the middle surface
$\mathbf{x}$ и $\mathbf{y}$ are positioned so that they have same angle between $\mathbf{x}$ и , $\mathbf{y}$

The origin of ($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$ are the same as it is at the intersection point of middle point line.

3-node Shell Element

($\mathbf{X}, \mathbf{Y}$ и $\mathbf{Z})$ - Global Cartesian fixed system

Natural system (non-normalized coordinate system).

is from Node 1 to Node 2.
is from Node 1 to Node 3.
Plane ( ) is in the middle surface of shell element и is normal of the middle surface.

($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$ - Local coordinate system (orthogonal, normalized elemental coordinate system).

$\mathbf{z}$ is normal of middle surface.
$\mathbf{x}$ is from Node 1 to Node 2.
$\mathbf{y}$ is orthogonal to $\mathbf{x}$ и ($\mathbf{x}$ и $\mathbf{y}$) are in the middle surface.

The origin of ($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$ are the same as it is at Node 1.

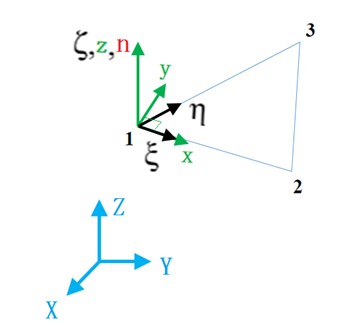
Figure 106:

Solids и Thick Shells (hexa)

Global system ($\mathbf{X}, \mathbf{Y}$ и $\mathbf{Z})$
Natural system ($\mathbf{r}, \mathbf{s}$ и $\mathbf{t})$
Local element coordinate system ($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$
Material system

Figure 107: Solids и Thick Shells (hexa)

($\mathbf{X}, \mathbf{Y}$ и $\mathbf{Z})$ - Global Cartesian fixed system

($\mathbf{r}, \mathbf{s}$ и $\mathbf{t})$ - Natural system (non-normalized coordinate system).

$\mathbf{r}$ is from the center of surface (1, 2, 6, и 5) to center of surface (4, 3, 7, и 8)
$\mathbf{s}$ is from the center of surface (1, 2, 3, и 4) to center of surface (5, 6, 7, и 8)
$\mathbf{t}$ is from the center of surface (1, 4, 8, и 5) to center of surface (2, 3, 7, и 6)

Plane ($\mathbf{r},\mathbf{t}$) is also in the middle surface (1’, 2’, 3’, и 4’).

$\mathbf{r}$ is also from middle point of Line 1’ и 2’ to middle point of Line 3’ и 4’.
$\mathbf{t}$ is also from middle point of Line 1’ и 2’ to middle point of Line 3’ и 4’
$\mathbf{n}$ is normal of middle surface (1’, 2’, 3’, и 4’)

($\mathbf{x}, \mathbf{y}$ и $\mathbf{z})$ - Local coordinate system (orthogonal, normalized elemental coordinate system).

Local coordinate system in middle surface (1’, 2’, 3’, и 4’) is the same as the local coordinate system in middle surface (1, 2, 3, и 4) for shell element. r in solid is the same as in shell element.

Tetra Elements

($\mathbf{r}, \mathbf{s}$ и $\mathbf{t})$ - Natural system (non-normalized coordinate system).

$\mathbf{r}$ is from node 4 to node 1
$\mathbf{s}$ is from node 4 to node 2
$\mathbf{t}$ is from node 4 to node 3

Figure 108: Tetra Elements

Material System

For shell element, anisotropic can be defined с property type 9, 10, 11, 16, 17, и 19, using a material system to describe the anisotropic. Vector $\mathbf{V}$ и angle $\phi$ requested to define material system. (See /PROP/TYPE9 Format below). Material direction ($\mathbf{m1}$ и $\mathbf{m2}$) presents the direction of different mechanic characters (Example: E-Modulus, shear Modulus, stress-strain behavior, damage, …) for anisotropic.

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$V_{X}$		$V_{Y}$		$V_{Z}$		$\phi$

Use vector $\mathbf{V}$ и angle $\phi$ material direction 1 ($\mathbf{m1}$) can be defined (along normal n project vector $\mathbf{V}$ to middle surface и get vector $\mathbf{V}$. Rotate angle $\phi$ of vector $\mathbf{V}$ then get material direction $\mathbf{m1}$. Material direction $\mathbf{m1}$ is normally the fiber direction. For composite, a different ply could be defined с one vector $\mathbf{V}$ и different $\phi$.

Second material axis $\mathbf{m2}$ is perpendicular to $\mathbf{m1}$ (except for /PROP/TYPE16, angle between $\mathbf{m1}$ и $\mathbf{m2}$ could be defined с α).

$\mathbf{n}$ is normal of shell middle surface

Figure 109:

In /PROP/TYPE11, $I_{orth}$ can determine the relative orientation of the material system.

$I_{orth}$ = 0 (default): The orthotropic direction follows the local co-rotational reference. The angle between $\mathbf{X}$ и $\mathbf{m1}$ is constant during the simulation. Internal force is computed in local frame и then rotated to the global system. This formulation is more accurate, if a large rotation occurs.
$I_{orth}$ = 1: The orthotropic direction is attached to the local isoparametric frame. The angle between и $\mathbf{m1}$ is updated during the simulation. It is updated in a way that projection of vector $\mathbf{m1}$ to и is always constant during the simulation. Pure shear could not well descripted с this method, but traction could well bedescribed. So, this method usually is used to defined fiber direction in airbag.

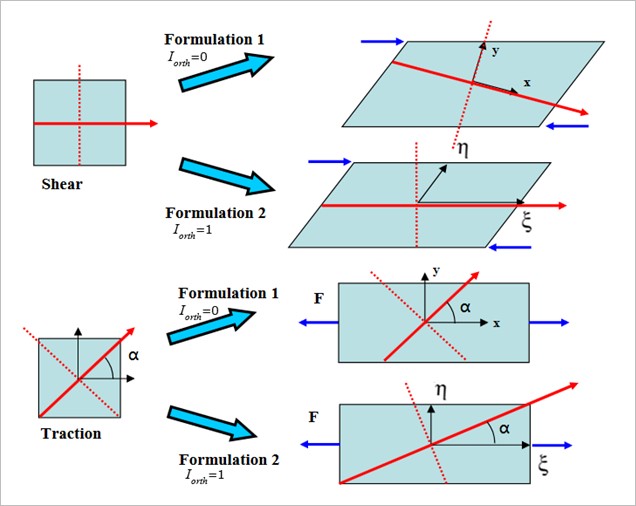
Figure 110:

For brick и thick shell elements, use the same process to determine the material direction и orthotropic direction ($I_{orth}$), like shell elements. In /PROP/TYPE6 (SOL_ORTH) use the option $I_{P}$ to determine the reference plane.

$\mathbf{i_{P}=0}$ Use Skew_ID.

$\mathbf{i_{P}=1}$ Plane ($\mathbf{r,s}$) + angle $\phi$

$\mathbf{i_{P}=2}$ Plane ($\mathbf{s,t}$) + angle $\phi$

$\mathbf{i_{P}=3}$ Plane ($\mathbf{t,r}$) + angle $\phi$

$\mathbf{i_{P}=11}$ Plane ($\mathbf{r,s}$) + orthogonal projection of references vector $\mathbf{V}$ on plane ($\mathbf{r,s}$)

$\mathbf{i_{P}=12}$ Plane ($\mathbf{s,t}$) + orthogonal projection of references vector $\mathbf{V}$ on plane ($\mathbf{s,t}$)

$\mathbf{i_{P}=13}$ Plane ($\mathbf{t,r}$) + orthogonal projection of references vector $\mathbf{V}$ on plane ($\mathbf{t,r}$)

Definition is the same for any $I_{solid}$ и $I_{frame}$ parameters
In the simplest case, material directions $\mathbf{m1, m2}$, и $\mathbf{m3}$ directly с skew ($I_{p} = 0$) are recommended
For $I_{p}$ > 0 the isoparametric, non-orthogonal system :math:``mathbf{r, s,}` и $\mathbf{t,}$ is used to determine material directions.

◦ First material axis $\mathbf{m1}$ is determined according to $I_{p}$.

◦ For example, for $I_{p}$ = 1

◦ The first material axis $\mathbf{m1}$ и $\mathbf{m2}$ is orthogonal и rotated be angel $\phi$ in the ($\mathbf{r'}$ и $\mathbf{s'}$) plane.

◦ The third material axis $\mathbf{m3}$ is normal of $\mathbf{m1}$ и $\mathbf{m2}$ plane (vector product $\mathbf{m1}$ и $\mathbf{m2}$).

Figure 111:

◦ The ($\mathbf{r', s',}$ и $\mathbf{t'}$) system is orthogonal и it is generated from non-orthogonal isoparametric system ($\mathbf{r, s,}$ и $\mathbf{t}$).

Figure 112: Orthogonalization of the Isoparametric System

Depending on $I_{solid}$ и $I_{frame}$ parameters, three definitions of systems are used in PRADIOS for hexa elements (8-noded bricks) using /PROP/TYPE6 (SOl_ORTH).

Global System Definition

Definition 1: Solids, $I_{solid}$ =1, 2, 17 + $I_{frame}$ =0, 1 (default)

Global system is used, no element system (non-co-rotational formulation) available.

Element System Definition

Definition 2: Solids, $I_{solid}$ =1, 2, 17 + $I_{frame}$ =2

Element system (с $I_{frame}$ =2 co-rotational formulation) is used.
Definition 3: Solids, $I_{solid}$ =14 or 24

$I_{frame}$ parameter has no effect. Element system is used, и co-rotational formulation defined already.

Note: If the co-rotational formulation is used, the orthotropic frame (defined с $I_{orth}$) keeps the same orientation с respect to the local (co-rotating) frame и is therefore also co-rotating.

Modeling Tools

Skew и Frame (/SKEW & /FRAME)

Skews и frames are used to define local directions.

These directions can be used to apply:

Boundary conditions
Concentrated load
Fixed velocity

To define:

Rigid link orientation
Rigid body added inertia frame
General spring reference frame
Beam type spring initial reference frame
Nodal time history output frame

Two reference definitions are available in PRADIOS:

Skew reference

It is a projection reference to define the local quantities с respect to the global reference. In fact, the origin of the skew remains at the initial position during the motion even though a moving skew is defined. In this case, a simple projection matrix is used to compute the kinematic quantities in the reference.

In Figure 113, imposed velocity is applied in Y direction. In /IMPVEL, skew is used. Then the imposed velocity is computed in the Y axis of global coordinate system и then projected onto the Y’ axis of local skew reference.

Figure 113: Skew Example

Frame reference

It is a mobile or fixed reference. The quantities are computed с respect to the origin of the frame which may be in motion or not depending on the kind of reference frame. For a moving reference frame, the position и the orientation of the reference vary in time during the motion.

The origin of the frame defined by a node position is tied to the node.

Frame measures relative motion whereas skew measures global motion и projects it to skew. Only few options use frame like imposed velocity, TH/NODE и others use skew.

In Figure 114, rotational velocity is applied around Z axis. In /LOAD/CENTRI, frame is used. Then rotational velocity is around Z’ axis of frame reference not in Z axis of global coordinate system anymore.

Figure 114: Frame Example

Sections (/SECT)

A section is used to measure the force, moment, и energy which are passing through a set of elements и nodes. The section displacements can also be saved to a file и used as imposed displacements in a smaller cut section model.

To define the section, the following are required:

A group of nodes и groups of elements. The nodes и elements can be selected by a user in /SECT. They can also be automatically selected by defining a section cut using /SECT с frame_ID, /SECT/PARAL, or /SECT/CIRCLE.
A local output system defined by selecting 3 points
A reference point to compute forces и moment

Figure 115: Definition of a Section for an Oriented Solid

Section Cutting Plane

In /SECT, the cutting plane is infinite и is defined by a group of elements и a group of nodes. The elements и nodes can be user-defined и should be along one row, if possible.

It is recommended to select all the nodes on one side of the element section.

Figure 116: Elements и Nodes Selected Manually

Alternatively, the section cut can be defined using a local system. The local system /FRAME/MOV is defined by picking three nodes on the section cut. In this case, the element groups contain all the elements in the area of the section, и the node group in /SECT is not used. The nodes и elements on the xy plane of the local system are automatically selected for the section calculation. The cutting plane is the xy plane of the local system.

Figure 117: Element Group (in orange) defined for a section cut defined using a local system

The nodes и elements that lie on the section cut are then output in the Starter output file.

NUMBER OF NODES. . . . . . . . .       40
 NODES:
6062   6064   6055    5074    6076     5895   6078    6173     6166     6136
6174   6181   6182    6219    6210     6220   6227    6228     6359     6358
. . .
      NUMBER OF SHELL ELEMENTS . . . . . . .               43
SHELL         N1          N2            N3           N4
   5819                0           1             1           0
   5820                0           1             1           0
   5826                0           0             1           0
   5839                0           1             1           0
. . .

In /SECT/PARAL, the cutting parallelogram is defined by three points M, M1, и M2 which define the two lines of the parallelogram. The element groups in the defined section should contain all the elements in the area of the parallelogram section. The nodes и elements used in the section calculation are automatically selected и output in the Starter output file, as shown previously for /SECT when a local system is used.

Figure 118: /SECT/PARAL Definition

In /SECT/CIRCLE, the cutting disk is defined by a point M, radius, и a normal vector. The element groups in the defined section should contain all the elements in the area of the circle section. The nodes и elements used in the section calculation are automatically selected и output in the Starter output file, as shown previously.

Figure 119: /SECT/CIRCLE Definition

All section types can cut solid, shell, truss, beam, и spring elements. Contact interfaces can also be selected.

When using /SECT с frame_ID, /SECT/PARAL, or /SECT/CIRCLE the nodes used for the section calculation will on the +z side of the selected elements. Since these nodes are automatically defined, the element groups can be defined by part и; thus, will not need to be redefined, if the part is remeshed.

Local System of Cutting Plane

A local system must be defined to compute the force и moment from the section.

In all three section types (/SECT, /SECT/PARAL, и /SECT/CIRCLE), three nodes must be selected to define the local system used for the section output. These three nodes should be nodes on the section plane so their position is updated when the section moves. The nodes node_ID₁, node_ID₂, и node_ID₃ define the local system as:

Nodes node_ID₁ и node_ID₂ define the local x-axis of the section.
Nodes node_ID₁, node_ID₂, и node_ID₃ define the local plane xy of the section.
The local y-axis is defined by projecting node_ID₃ perpendicular to the local x-axis.
The intersection of the local x- и y-axis is then the origin of the system.
The section normal is the local z-axis which is perpendicular to thexy plane.

Figure 120: Section local system defined using nodes

When creating a /SECT in HyperMesh, these three nodes are automatically selected for the user. If they are manually selected, it is recommended to select nodes that belong to the group of nodes used in the section calculation. This will allow the local system to move as the section deforms.

Alternatively, in /SECT if the 3 nodes are not defined и instead a frame_ID is defined then the xy plane of the /FRAME/MOV is used as the local system. When defining the /FRAME/MOV it is recommended to use nodes that belong to the group of nodes used in the section calculation.

Force и Moment Computation

The section force is the sum of nodal force coming from the selected elements.

\[F=\sum f_{i} \tag{47}\]

The normal Force FN of the section is the component of section force in the normal direction и tangent force FT of the section is the component of section force in cutting plane.

Figure 121: Normal section force и tangent section force in section

The section moment is the sum of nodal forces coming from the selected element multiplied by the distance to the local coordinate system center.

\[M=\sum m_{i}+\sum ON_{i}\times f_{i} \tag{48}\]

Figure 122: Resultant of force и moment for a node

Moments are computed с respect to the section center defined by the parameter $I_{frame}$. Options for the output system center include local system origin, geometric center, center of gravity, и global system origin. The output system can be either the local system or the global system.

Figure 123: $I_{frame}$ =0 Local system и origin used for section output

Figure 124: $I_{frame}$ =1 Local system с the origin as the geometric center of the section

Figure 125: $I_{frame}$ =2 Local system с the origin as the center of gravity of the section

Figure 126: $I_{frame}$ =3 Local system с the global origin as the center

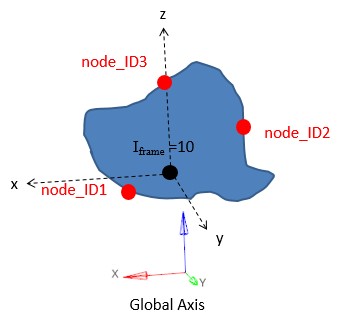
Figure 127: $I_{frame}$ =10 Global system с the center as the local system origin

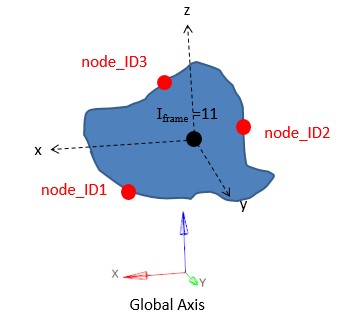
Figure 128: $I_{frame}$ =11 Global system с the origin as the geometric center of the section

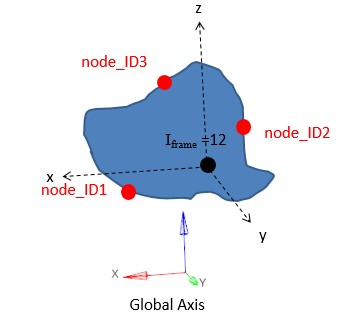
Figure 129: $I_{frame}$ =12 Global system с the origin as the center of gravity of the section

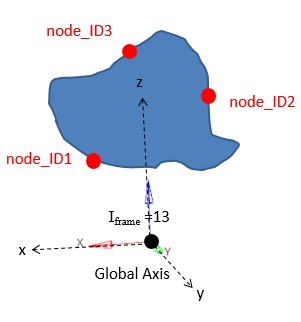
Figure 130: $I_{frame}$ =13 Global system с the global origin as the center

Приложения	Материал	Свойство	Песочные часы	Количество	Толщина	Пласти чность
Базовый сбой	2	1	1	(global)	Постояный	Радиалный
Авария с трапециевидны ми оболочками и с глобальным вращением	2	1	3(c) or `QEPH`	(global)	Постояный	Радиалный
Авария с возвратной пружиной средней точности	2/36	1	1	3	Постояный	итерация
Авария с возвратной пружиной высокая точность	2/36	1	3(c) or `QEPH`	3	Переменая	итерация
Авария с разрушением пластичного материала	2/36 (a)	1	1	5	Переменая	итерация
Авария высокого качества	2/36 (a)	1	3(c) or `QEPH`	5	Переменая	итерация
Авария с разрушением хрупкого материала	27	11	1	3/5	Переменая	итерация
Лобовое стекло	27	11	1	3+1+3(b)	Переменая	итерация
Мембрана или ткань	1/2/19/36	1	1	1	cst/var	rad/iter
композитный	25	9/10/11	1	1 to 30	не делает	не делает
Модель с локальным возбуждением в виде песочных часов	2/…	1	3(c) or `QEPH`	0/3/5
Модель с низкой пластичностью и низкими скоростями	2/…	1	3(c) or `QEPH`	3/5

Запуск PRADIOS

Из команднной консоли

Ввод имя файла

Часто используемые параметры запуска

Все доступные варианты запуска

Решения управление

Из сценария моделирования

Из HyperMesh

Запуск исполняемого файла напрямую

Коды выхода Starter и Engine

Аргументы стартовой командной строки

-help Argument

-version Argument

-input [FILE] Argument

-nspmd [SPMD DOMAIN NUMBER] Argument

-nthread [SMP THREAD NUMBER] Argument

-notrap Argument

-check Argument

-outfile=[output path] Argument

-HSTP_WRITE Argument

-HSTP_READ Argument

-rseed [seed] Argument

-rxalea [xalea] Argument

-dylib [FILE] Argument

-mds libpath [PATH] Argument

Аргумент командной строки механизма

-help Argument

-version Argument

-input [FILE] Argument

Пример

-nthread [SMP THREAD NUMBER] Argument

Пример

Общее поведение, обработка ошибок

Согласованность опций MPI и PRADIOS

-notrap Argument

-norst Argument

-outfile=[output path] Argument

Пример

-dylib [FILE] Argument

-mds libpath [PATH] Argument

Процесс решения

Рекомендации по использованию нескольких ядер

Одна рабочая станция

Компьютерный кластер

Две или три рабочие станции

Размер модели

Используйте другое количество ядер

Передовые методы

Управляющий файл (C-файл)

Несколько файлов движка

Определите и запустите несколько входных файлов механизма

Файл контрольной точки

Вычисление одинарной точности

Запустите симуляцию с одинарной точностью

Явный структурный анализ методом конечных элементов

Шаг времени

Временной шаг элемента

Узловой шаг по времени

Глобальный временной шаг

Временной шаг контактного интерфейса

Выходные данные временного шага из модели

Начальный временной шаг модели

Шаг выполнения модели по времени

Методы управления временным шагом

Узловое управление шагом времени

/DT/NODA/CST

/DT/NODA/SET

/DT/NODA/STOP

Управление шагом времени элемента

/DT/Eltyp/CST

/DT/Eltyp/DEL

/DT/Eltyp/STOP

Контактный интерфейс управления временным шагом

/DT/INTER/CST

/DT/INTER/DEL

/DT/INTER/STOP

/DT/INTER/AMS

Расширенное массовое масштабирование (РММ)

Увеличьте скорость вычислений и поддерживайте точность

14.0 Новые функции AMS