/MAT/LAW28 (HONEYCOMB)

Radioss 2025.1

Jump to main content

Этот закон описывает трехмерный нелинейный элластично-пластичный материал, обычно используемый для моделирования материалов типа “соты” или пеноматериала.

Формат

• /MAT/LAW28 (HONEYCOMB)

• Блок формат ключевого слова

• Нелинейное элластично-пластичное поведение может быть задано для каждого ортотропного направления и сдвига как функция деформации или объемной деформации. Все степени свободы независимы, и материал полностью сжимаем. Критерии разрушения на основе напряжения и сдвиговой деформации могут быть заданы.

Блок формата ключевого слова:

/MAT/LAW28/mat_ID/unit_ID or /MAT/HONEYCOMB/mat_ID/unit_ID
мат_название ρ_i E_11 E_22 E_33 G_12 G_23 G_31

Напряжение сдвига возникает в нормальных направлениях 11, 22 и 33:

fct_ID11 fct_ID22 fct_ID33 Iflag1 Fscale11 Fscale22 Fscale33 ε_max11 ε_max22 ε_max33

Сдвиговая деформация возникает в направлениях 12, 23 и 31:

fct_ID12 fct_ID23 fct_ID31 Iflag2 Fscale12 Fscale23 Fscale31 ε_max12 ε_max23 ε_max31

Определение

Поле	Содержание	Пример в единицах СИ
mat_ID	Идентификатор материала. (Целое число, максимум 10 знаков)
unit_ID	Идентификатор единицы. (Целое число, максимум 10 знаков)
mat_title	Название материала. (Символы, максимум 100 знаков)
ρ_i	Начальная плотность материала. (Действительное число) [кг/м³]
E_11, E_22, E_33	Модуль Юнга в ортотропном измерении 1, 2, 3. (Действительное число) [Па]
G_12, G_23, G_31	Модуль сдвига в направлении 12, 23, 31. (Действительное число) [Па]
fct_ID11, fct_ID22, fct_ID33	Идентификаторы функций напряжения текучести в направлениях 11, 22, 33. (Целое число)
Iflag	Формулировка деформации для функций текучести. = 0 (по умолчанию) функция объемных деформаций, = 1 функция деформации, = -1 функция отрицательной деформации. (Целое число)
Fscale11, Fscale22, Fscale33	Коэффициенты масштабирования функций текучести в направлениях 11, 22, 33. По умолчанию = 1.0 (Действительное число) [Па]
ε_max11, ε_max22, ε_max33	Деформация разрушения при растяжении в направлениях 11, 22, 33. (Действительное число)

Пример (Сталь):

#RADIOSS STARTER
#---1----|---2----|---3----|---4----|---5----|---6----|---7----|---8----|---9----|---10----|
/UNIT/1
единица для мат
Mg mm s
#---1----|---2----|---3----|---4----|---5----|---6----|---7----|---8----|---9----|---10----|
/MAT/HONEYCOMB/1/1
Сталь
# RHO_I
7.8E-9
# E_11 E_22 E_33
200000 200000 200000
# G_12 G_23 G_31
100000 100000 100000
fct_ID11 fct_ID22 fct_ID33 Iflag1 Fscale11 Fscale22 Fscale33
1 1 1 0 0 0 0
# Eps_max11 Eps_max22 Eps_max33
0 0 0
fct_ID12 fct_ID23 fct_ID31 Iflag2 Fscale12 Fscale23 Fscale31
2 2 2 0 0 0 0
# Eps_max12 Eps_max23 Eps_max31
0 0 0
#---1----|---2----|---3----|---4----|---5----|---6----|---7----|---8----|---9----|---10----|

Комментарии

Этот закон материала требует твёрдых ортотропных свойств /PROP/TYPE6 (SOL_ORTH). Материал совместим с элементами гекса и тетра, включая элементы тетраэдра с 10 узлами. См. Материальную совместимость для получения дополнительной информации о совместимости.

Ортотропные координатные системы материала для каждого элемента (направления 1, 2 и 3) задаются в карточке свойств /PROP/TYPE6 либо через заданную систему координат, либо относительно системы координат элемента.

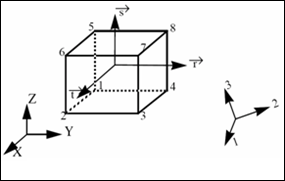
Все степени свободы элемента полностью независимы.

Пример для эластичного случая:

σ₁₁ = E₁₁ * ε₁₁ σ₁₂ = G₁₂ * ε₁₂ σ₂₂ = E₂₂ * ε₂₂ σ₂₃ = G₂₃ * ε₂₃ σ₃₃ = E₃₃ * ε₃₃ σ₃₁ = G₃₁ * ε₃₁

В каждой из направлений напряжения/компрессии и сдвига истинное напряжение как функция истинной объемной деформации μ или истинной деформации ε можно задавать.

См. также:

Материальная совместимость, Модели разрушения (Руководство по справке), Нелинейные псевдопластические ортотропные материалы (LAW28, 50 и 68) (Теоретическое руководство).