/MAT/LAW36 (PLAS_TAB)

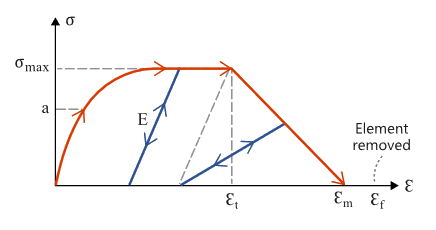
_images/f8bafd44_mat_law36_damage_yield.png

Данный закон моделирует изотропный эластопластичный материал, используя функции, заданные пользователем, для части кривой напряжение-деформация, связанной с упрочнением (например, напряжение против пластической деформации) для различных скоростей деформации. Для твердых элементов и SPH элементы, этот материал может учитывать нелинейную зависимость между давлением и плотностью при условии наличия соответствующего уравнения состояния.

Формат

/MAT/LAW36
/mat_ID/unit_ID or /MAT/PLAS_TAB/mat_ID/unit_ID
mat_title
ρ_i E ν ε_pmax ε_t ε_m N_funct F_smooth C_hard F_cut ε_f VP fct_IDp Fscale fct_IDE E_inf C_E N_funct > 0: Read 1 + INT((N_funct-1)/5) cards
fct_ID1 fct_ID2 fct_ID3 fct_ID4 fct_ID5 N_funct > 0: Read 1 + INT((N_funct-1)/5) cards
Fscale1 Fscale2 Fscale3 Fscale4 Fscale5 N_funct > 0: Read 1 + INT((N_funct-1)/5) cards
ε̇1 ε̇2 ε̇3 ε̇4 ε̇5

Определение

  • mat_ID: Идентификатор материала. (Целое число, максимум 10 знаков)

  • unit_ID: Идентификатор единицы. (Целое число, максимум 10 знаков)

  • mat_title: Название материала. (Символы, максимум 100)

  • ρ_i: Начальная плотность. (Реальное число) [кг/м³]

  • E: Модуль Юнга. (Реальное число) [Па]

  • ν: Коэффициент Пуассона. (Реальное число)

  • ε_pmax: Максимальная пластическая деформация. (Реальное число)

  • ε_t: Значение растяжимой деформации, при котором начинается снижение напряжения. (Реальное число)

  • ε_m: Максимальная растяжимая деформация, при которой напряжение в элементе равняется нулю. (Реальное число)

  • N_funct: Количество функций (1 ≤ N_funct ≤ 100). (Целое число)

  • F_smooth: Параметр сглаживания напряжения. (Целое число). - 1 (По умолчанию): Сглаживание с линейной интерполяцией. - 2: Сглаживание с натуральным логарифмом.

  • C_hard: Коэффициент упрочнения. (Реальное число). - 0: Полное изотропное упрочнение. - 1: Упрочнение по модели Прагера-Циглера.

  • F_cut: Частота отсечения для фильтрации скорости деформации. (Реальное число) [Гц]

  • VP: Параметр выбора типа скорости деформации. (Целое число).

  • ε_f: Значение растяжимой деформации для удаления элемента. (Реальное число).

  • fct_IDp: Функция фактора текучести относительно давления. (Целое число).

  • Fscale: Масштабный коэффициент для фактора текучести в fct_IDp. (Реальное число) [Па]

  • fct_IDE: Идентификатор функции для масштаба модуля Юнга. (Целое число).

  • E_inf: Насытный модуль Юнга для бесконечной пластической деформации. (Реальное число).

  • C_E: Параметр для эволюции модуля Юнга. (Реальное число).

Пример (сталь)

#RADIOSS STARTER
/UNIT/1
g  mm  ms
#  2. MATERIALS:
/MAT/PLAS_TAB/1/1
MAT_TABULATED_STEEL_EXAMPLE
# Init. dens.
    0.0078
# E  Nu  Eps_p_max Eps_t Eps_m
 221000.0  0.3
# N_funct  F_smooth  C_hard  F_cut   Eps_f  VP
     5            1
# fct_IDp  Fscale   Fct_IDE  E_inf  C_E

# func_ID1  func_ID2  func_ID3  func_ID4  func_ID5
     1         2         3         4         4
# Fscale_1  Fscale_2  Fscale_3  Fscale_4  Fscale_5
     1.0      1.0      1.0      1.0    1.001
# Eps_dot_1 Eps_dot_2 Eps_dot_3 Eps_dot_4 Eps_dot_5
     0.0     0.01     0.1      1.0     1000.0

Комментарии

Первой точкой функций текучести (пластическая деформация против напряжения) должна быть нулевая пластическая деформация. Функции текучести должны быть строго положительными. Напряжение должно быть либо постоянным, либо возрастающим (не должно быть размягчения, чтобы избежать численных неустойчивостей).

Удаление элемента: - Как только ε_p (пластическая деформация) достигает ε_pmax в одной точке интеграции, элемент удаляется. - Если ε_1 (наибольшее главное напряжение) достигает ε_t, то напряжение текучести уменьшается по следующей формуле:

\[\sigma_{Yd} = \sigma_Y \frac{\varepsilon_m - \varepsilon_1}{\varepsilon_m - \varepsilon_t}\]
_images/93bc1877_matx36_image1.svg

Для отдельных материалов, таких как металлы, общее напряжение определяется умножением номинального напряжения текучести на фактор текучести, соответствующий реальному давлению. Если ε̇ ≤ ε̇_n, напряжение текучести интерполируется между f_n и f_{n-1}.

Более точная эволюция модуля Юнга (если fct_IDE > 0) задается кривой, определяющей масштабный коэффициент, который уменьшается с накопленной эквивалентной пластической деформацией:

\[E(t) = f(\bar{\varepsilon}_p)E\]

Если начинаемое значение шкалы равно 1, то оно уменьшается. Если fct_IDE = 0, модуль Юнга рассчитывается как:

\[E(t) = E - (E - E_{inf})(1 - exp(-C_E\bar{\varepsilon}_p))\]

Где E и E_{inf} - это начальные и асимптотические значения модуля Юнга соответственно, а bar{varepsilon}_p - накопленная эквивалентная пластическая деформация.

Note

Если fct_IDE = 0 и C_E = 0, модуль Юнга E остается постоянным.

См. также

  • Справочник по совместимости материалов

  • Модели отказа

  • Закон Джонсона-Кука (/MAT/LAW2)

  • Эластопластичный материал с линейными кусочными функциями и квадратичными законами (/MAT/LAW36 и /MAT/LAW60)

  • RD-E: 1101 Характеризация закона эластопластичной модели

  • RD-E: 4900 Удар птицы о лобовое стекло

  • RD-V: 0240 Табулированный материал (LAW36)