/MAT/LAW38 (VISC_TAB)

Описание

Данный закон описывает табличную модель вязко-упругого пенного материала и может использоваться только с объемными элементами.

Формат

/MAT/LAW38/mat_ID/unit_ID or /MAT/VISC_TAB/mat_ID/unit_ID
mat_title
ρ_i     E_0     ν_t     ν_c     R_ν     Iflag     Itota     β     H     R_D     K_R     K_D     θ     K_air
fct_ID_p     Fscale_P     P_0     R_P     P_max     Φ
fct_ID_ul     Fscale_unload     ε̇_unload     a     b     N_funct     CUToff     Iinsta
E_final     ε_final     λ     Visc     Tol
Fscale_i     ε̇_i     fct_ID_iL     fct_ID_iul
...

Поле mat_ID — идентификатор материала (целое число, максимум 10 цифр).

Пример (Пена)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/VISC_TAB/1/1
Foam
#              RHO_I
               2E-10
#                E_0                nu_t                nu_c                 R_V     Iflag     Itota
                 200                   0                   0                   0         0         0
#               Beta                   H                 R_D       K_R       K_D                Teta
                   0                   0                   0         0         0                   0
#    K_air  fct_ID_p            Fscale_P
         0         0                   1
#                 P0                  Rp                Pmax                 Phi
                   0                   0                   0                   0
#funID_unl                 Fscale_unload        Eps_._unload                   a                   b
         0                             0                   0                   0                   0
#  N_funct                       CUT_off   I_insta
         1                             0         0
#            E_final           Eps_final              Lambda                Visc                 Tol
                   0                   0                   0                   0                   0
#      Fscale_i
                   1
#      Eps_._i
                   0
#    func_ID_iload
         4
#    func_ID_iunload
         0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/4
function_4
#                  X                   Y
                  -1                -200
                   1                 200
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END

Комментарии

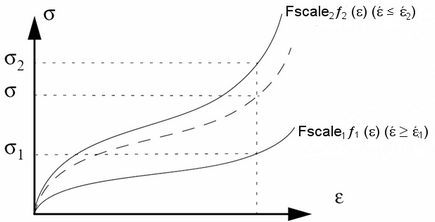
Инженерное напряжение по отношению к инженерной деформации может быть введено как функции для различных скоростей деформации. Напряжение и деформация считаются положительными при сжатии и отрицательными при растяжении. По умолчанию (Itota=0) поведение при растяжении является линейно-упругим с использованием модуля Юнга E_0. Если Itota=1, поведение должно быть введено с использованием функций fct_ID_iL с кривой напряжения и деформации, определенной как в сжатии, так и в растяжении.

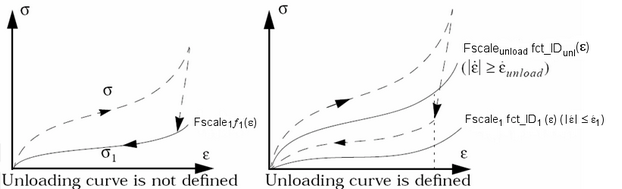
Если кривая разгрузки не определена (fct_ID_iul=fct_ID_ul=0), напряжение вычисляется на основе первой входной функции нагрузки fct_ID_1L.

См. также

• Совместимость материалов

• Модели разрушения (Руководство по ссылкам)

• Табличное зависимое от скорости напряжения для вязкоупругих материалов (Теоретическое руководство)