/MAT/LAW14 (COMPSO)

Руководство по справочнику PRADIOS

Этот закон описывает ортотропный твердый материал с использованием формулировки Цая-Ву, который в основном предназначен для моделирования однонаправленных композитов. Этот материал считается 3D ортотропно-упругим до достижения критерия Цая-Ву, после чего материал становится нелинейным.

_images/mat_law12_distortion.png

Закон /MAT/LAW14 (COMPSO) предназначен для представления ортотропного твердого материала с использованием формулировки Цая-Ву. Он в основном предназначен для моделирования однонаправленных композитов. Материал считается 3D ортотропно-упругим до достижения критерия Цая-Ву, после чего он становится нелинейным. Нелинейность в направлении 3 такая же, как и в направлении 2, чтобы представить поведение матричного материала композита. Критерий Цая-Ву может зависеть от пластической работы и скорости деформации в каждом из ортотропных направлений и при сдвиге для моделирования упрочнения материала. Доступен ортотропный критерий, основанный на напряжении, для хрупкого повреждения и разрушения.

Format

` /MAT/LAW14/mat_ID/unit_ID /mat_ID/COMPSO /unit_ID/mat_title ρi E11 E22 E33 ν12 ν23 ν31 G12 G23 G31 σt1 σt2 σt3 δ B n fmax Wpref `

Определения

Пример (Металл)

#RADIOSS STARTER
/UNIT/1
unit for mat kg cm ms
/MAT/COMPSO/1/1
Metal
             .0078
                       10                 100                   1
                        0                   0                   0
                        0                   0                   0
                 1E31                1E31                1E31                   0
                 1E31                1E31                1E31                   0
                 1E31                1E31                1E31                1E31
                 1E31                1E31                1E31                1E31
                        0                   0                   0                   0         0
#ENDDATA
/END

Комментарии

Этот материал требует ортотропного твердотельного свойства (/PROP/TYPE6 (SOL_ORTH), /PROP/TYPE21 (TSH_ORTH) или /PROP/TYPE22 (TSH_COMP)). Он может быть использован только с твердыми элементами для 3D анализа. Этот закон совместим с тетраэдрами на 10 узлов и тетраэдрами на 4 узла. Ортотропные направления материала задаются в записях свойств.

Деформации и напряжения связаны как:

\[ \begin{align}\begin{aligned}ε_{11} = \frac{σ_{11}}{E_{11}} - \frac{ν_{21} σ_{22}}{E_{22}} - \frac{ν_{31} σ_{33}}{E_{33}}\\ε_{22} = \frac{σ_{22}}{E_{22}} - \frac{ν_{21} σ_{11}}{E_{11}} - \frac{ν_{32} σ_{33}}{E_{33}}\\ε_{33} = \frac{σ_{33}}{E_{33}} - \frac{ν_{13} σ_{11}}{E_{11}} - \frac{ν_{23} σ_{22}}{E_{22}}\\γ_{12} = \frac{σ_{12}}{2G_{12}}\\γ_{23} = \frac{σ_{23}}{2G_{23}}\\γ_{31} = \frac{σ_{31}}{2G_{31}}\\\frac{ν_{21}}{E_{22}} = \frac{ν_{12}}{E_{11}}\\\frac{ν_{32}}{E_{33}} = \frac{ν_{23}}{E_{22}}\\\frac{ν_{13}}{E_{11}} = \frac{ν_{31}}{E_{33}}\end{aligned}\end{align} \]

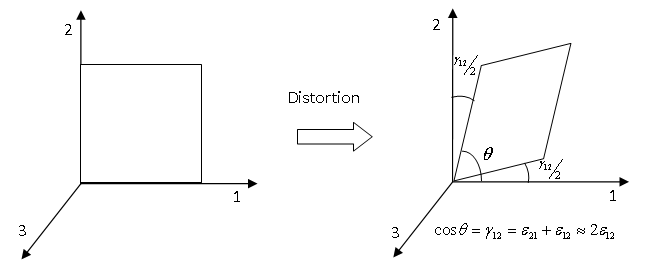
Где: \(ε_{ij}\) - деформации, \(σ_{ij}\) - напряжения, \(γ_{12}\), \(γ_{23}\), и \(γ_{31}\) - искажения в соответствующих направлениях материалов.

Критерий Цая-Ву

Материал считается упругим до тех пор, пока не будет выполнен критерий Цая-Ву. После превышения предельного критерия Цая-Ву F(Wp*, ε̇) материал становится нелинейным.

При условиях: - F(σ) < F(Wp*, ε̇): упругий - F(σ) > F(Wp*, ε̇): нелинейный

Где F(σ) в элементе для критерия Цая-Ву вычисляется как:

\[F(σ) = F_1σ_1 + F_2σ_2 + F_3σ_3 + F_{11}σ_1^2 + F_{22}σ_2^2 + F_{33}σ_3^2 + F_{44}σ_{12}^2 + F_{55}σ_{23}^2 + F_{66}σ_{31}^2 + 2F_{12}σ_1σ_2 + 2F_{23}σ_2σ_3 + 2F_{13}σ_1σ_3\]

Коэффициенты критерия Цая-Ву определяются по пределам, когда материал становится нелинейным, в направлениях 1, 2, 3 или 12, 23, 31 (сдвиг) при сжатии или растяжении.

\[ \begin{align}\begin{aligned}F_1 = \frac{-1}{σ_{1yc}} + \frac{1}{σ_{1yt}}\\F_2 = \frac{-1}{σ_{2yc}} + \frac{1}{σ_{2yt}}\end{aligned}\end{align} \]

…

Поведение в направлениях 2 и 3 предположительно одинаковое, чтобы представить матрицу композита.

Упрочнение материала определяется как:

\[F(Wp*, ε̇) = [1 + B(Wp*)^n] \cdot [1 + c \cdot \ln(\frac{ε̇}{ε̇_0})]\]

Где: - Wpref - эталонная пластическая работа - B - параметр пластического упрочнения - n - показатель пластического упрочнения - c - коэффициент скорости деформации

При условиях ICC:

  • ICC = 1: fmax(1 + c cdot ln(frac{ε̇}{ε̇_o}))

  • ICC = 2: fmax

Пример (Металл)

#RADIOSS STARTER … /END