/MAT/LAW21 (DPRAG)

Базовый Формат Ключевых Слов

Этот закон, основанный на критериях текучести Друкера-Прагера, используется для моделирования материалов с внутренним трением, таких как камень-бетон. Пластическое поведение этих материалов зависит от давления в материале.

Этот закон аналогичен /MAT/LAW10 (DPRAG1), единственное отличие заключается в том, что в этом законе давление задается как функция объемного деформирования, заданная пользователем. Этот закон совместим только с твердыми элементами.

Формат

/MAT/LAW21
/ mat_ID / unit_ID  или  /MAT/DPRAG
/ mat_ID / unit_ID
mat_title
ρ_i
E
ν
A_0 A_1 A_2 A_max fct_IDf K_t Fscale P ΔP_min P_ext B μ_max

Определение

Пример (Песок)

#RADIOSS STARTER
/UNIT/1
unit for mat
                  Mg                  mm                   s
/MAT/DPRAG/1/1
Sand
#        Init. dens.
              1.6E-9
#                  E                  Nu
                 100                  .3
#                 A0                  A1                  A2                Amax
                1E-7                .001                   1                   0
#       If                            Kt              Fscale
         2                             1                   0
#              P_min
           -1.5E-4
#                  B              Mu_max
                  80                  .4
/FUNCT/2
Sand
#                  X                   Y
                  -1                   0
                   0                   0
                  .1                 1000
                  .2                 2500
                  .3                 5000
                  .4                10000
#ENDDATA

Комментарии

Гидродинамическое поведение задается функцией, заданной пользователем \(P = f(ν)\), где \(P\) - давление в материале; \(μ\) - объемное деформирование с \(μ = \cfrac{ρ}{ρ_0} - 1\).

Критерии текучести Друкера-Прагера используют модифицированные критерии текучести Мизеса, чтобы учесть влияние давления для массивных структур:

\(F = J_2 - (A_0 + A_1 P + A_2 P^2)\)

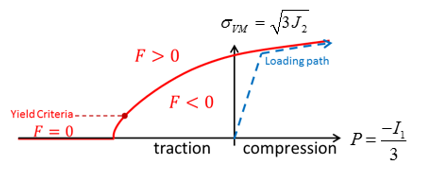
Где, - \(J_2\) - второй инвариант девиаторного напряжения, где \(\sigma_{VM} = \sqrt{3J_2}\) - \(P\) - давление, где \(P = - \cfrac{I_1}{3}\) (\(I_1\) - первый инвариант напряжений)

Коэффициенты пластичности материала \(A_0\), \(A_1\), \(A_2\).

Если \(A_1 = A_2 = 0\), критерии текучести соответствуют Мизесу (\(\sigma_{VM} = \sqrt{3A_0}\)).

Рекомендуется установить объемный модуль разгрузки, \(B\), равным начальному наклону функции, описывающей \(P(μ)\), и объемный модуль растяжения, \(K_t\), равным 1/100 объемного модуля разгрузки \(B\), причем \(K_t\) должен быть положительным.

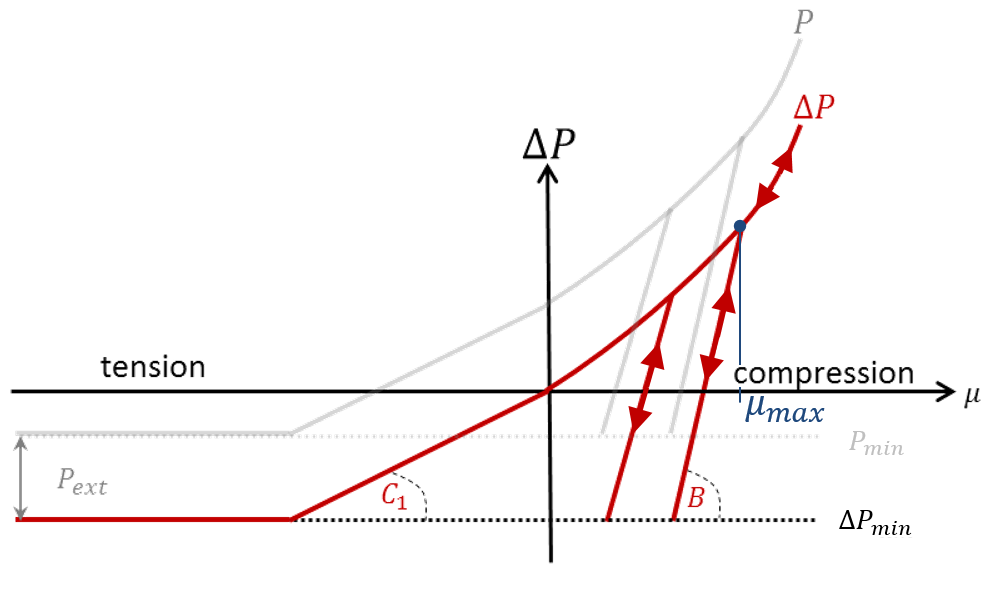
В случае формулировки относительного давления требуется внешнее давление. В этом конкретном случае критерии текучести и интеграция энергии требуют значения общего давления. Radioss выводит давление, которое является относительным к \(P_{ext}\). Вы можете получить значение общего давления из: \(P = P_{ext} + ΔP\).

Ограничение общего давления выводится из: \(P_{min} = P_{ext} + ΔP_{min}\).

Если \(P_{ext} = 0\), то результат вывода будет равен общему давлению: \(P = ΔP\) и \(P_{min} = ΔP_{min}\).

\(B\) - это объемный модуль разгрузки. Если \(B\) задан, то он должен превышать любой наклон \(\cfrac{dP}{dμ}\) в пределах \([0, μ_{max}]\).

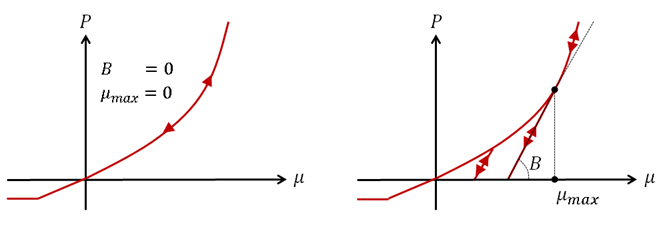
Если \(B = 0\) и \(μ_{max} = 0\), пути загрузки и разгрузки одинаковы.

Если \(B = 0\) или \(μ_{max} \neq 0\), значение по умолчанию для \(B\) - это

\(B = \cfrac{dP}{dμ}|_{μ_{max}}\).

Если \(B \neq 0\) или \(μ_{max} = 0\), значение по умолчанию для \(μ_{max}\)

Друкера-Прагера (LAW10 и LAW21) (Теоретическое руководство)

Смотрите также: Совместимость материалов, модели отказа (Справочное руководство).