/MAT/LAW22 (DAMA)
Radioss 2025.1
Эластопластические материалы
Материал /MAT/LAW22 (DAMA) идентичен материалу Джонсона-Кука (/MAT/LAW2) за исключением того, что материал повреждается, если пластические деформации достигают заданного пользователем значения (ε_dam). Этот закон может применяться как к оболочечным, так и к объемным элементам.
Определение формата блока
Формат:
`
/MAT/LAW22
/mat_ID/unit_ID или /MAT/DAMA/mat_ID/unit_ID
мат_title ρi E ν a b n ε_pmax σ_max0 c ε̇0 ICC ε_dam Et
`
Определение полей
mat_ID: Идентификатор материала (Целое число, до 10 знаков).
unit_ID: Идентификатор единиц измерения (Целое число, до 10 знаков).
mat_title: Название материала (Строка, до 100 символов).
ρi: Начальная плотность (Реальное число) [кг/м^3].
E: Модуль Юнга (Реальное число) [Па].
ν: Коэффициент Пуассона (Реальное число).
a: Предел текучести - должен быть строго положительным (Реальное число) [Па].
b: Параметр упрочнения (Реальное число) [Па].
n: Показатель упрочнения (Реальное число).
ε_pmax: Максимальная пластическая деформация, по умолчанию = 10^30 (Реальное число).
σ_max0: Максимальное напряжение, по умолчанию = 10^30 (Реальное число) [Па].
c: Коэффициент скорости деформации, по умолчанию = 0.00 (Реальное число).
ε̇0: Относительная скорость деформации (Реальное число) [1/с].
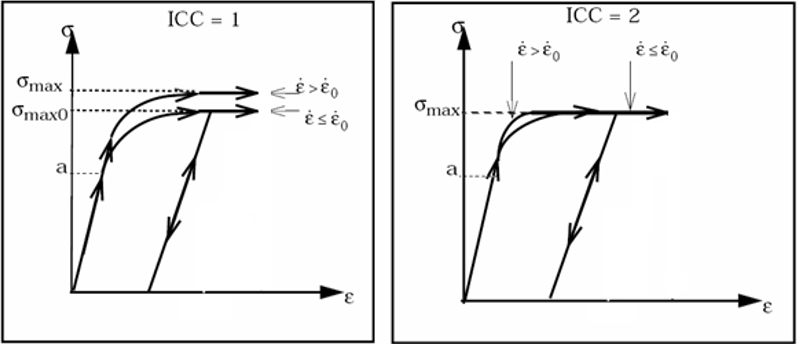
ICC: Флаг вычисления скорости деформации (Целое число). - 0 (по умолчанию): Нет эффекта скорости деформации - 1: Эффект скорости деформации на σ_max. - 2: Нет эффекта скорости деформации на σ_max.
ε_dam: Модель повреждения начинается при ε_dam, по умолчанию = 0.15 (Реальное число).
Et: Наклон убывания упрочнения (-E < Et <= 0), по умолчанию = 0.00 (Реальное число) [Па].
Пример (Алюминий)
```radioss #RADIOSS STARTER /UNIT/1 unit for mat
g mm ms
/MAT/DAMA/1/1 Alu # RHO_I
.0027
- # E Nu
70000 .3
- # a b n Eps_max SIGMA_max0
100 0 1 .2 100
- # c Eps_dot_0 ICC
0 0 0
- # Eps_dam E_t
.1 -2000
Комментарии
Повреждение изотропно и имеет одинаковое влияние при растяжении и сжатии.
[ sigma = (a + b varepsilon^n_p)(1 + c ln frac{varepsiloṅ}{varepsiloṅ_0}) ]
Где: - ε_p: Пластическая деформация - ε̇: Скорость деформации - ICC: флаг влияния скорости деформации на максимальное напряжение материала σ_max.
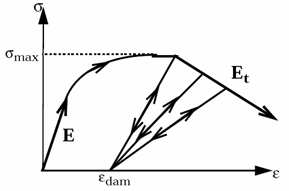
Повреждение появляется, когда деформация превышает максимальное значение ε_dam: - 0 ≤ δ ≤ 1 - Если ε < ε_dam, то δ = 0, закон 22 идентичен закону MAT/LAW2. - Если ε ≥ ε_dam, то:
E_dam = (1 - δ)E
ν_dam = 0.5δ + (1 - δ)ν
Для объемных элементов закон повреждения применяется только к девиаторному тензору напряжений s_ij: - G_dam = E_dam / 2(1 + ν_dam).
Когда ε_p достигает ε_pmax в одной интеграционной точке, зависит от типа элемента: - Оболочечные элементы: соответствующий оболочечный элемент удаляется. - Объемные элементы: девиаторное напряжение соответствующей интегральной точки постоянно устанавливается в 0, однако объемный элемент не удаляется.
См. также
Материал Совместимость (Материалное руководство) Модели повреждения (Теория) Модели повреждения (Руководство по материалам)