/MAT/LAW32 (HILL)

Ключевое слово в формате блока Этот закон: описывает ортотропный пластический материал Хилла. Это применимо только для оболочки элементов. Этот закон отличается от ЗАКОНА43. (HILL_TAB) только при вводе доходности стресс.

Формат


/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID	/MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID
mat_title	mat_title	mat_title	mat_title	mat_title	mat_title	mat_title	mat_title	mat_title	mat_title
\(\rho_{i}\)	\(\rho_{i}\)
E	E	\(\nu\)	\(\nu\)
a	a	\(\epsilon_{0}\)	\(\epsilon_{0}\)	n	n	\(\epsilon_{p}^{max}\)	\(\epsilon_{p}^{max}\)	\(\sigma_{max0}\)	\(\sigma_{max0}\)
\(\dot{\epsilon}_{0}\)	\(\dot{\epsilon}_{0}\)	m	m
r00	r00	r45	r45	r90	r90			Доходность0

Определение

Поле	Содержание	Пример единицы СИ
mat_ID	Идентификатор материала.(Целое число, максимум 10 цифры)
unit_ID	Идентификатор объекта.(Целое число, максимум 10 цифр)
mat_title	Название материала.(Символ, максимум 100 персонажи)
\(\rho_{i}\)	Начальная плотность.(Реальная)	\([\frac{kg}{m^{3}}]\)
E	Модуль Юнга.(Реальный)	\([Pa]\)
\(\nu\)	Коэффициент Пуассона.(Реальный)
a	Параметр доходности.(Реальный)	\([Pa]\)
\(\epsilon_{0}\)	Параметр закалки.(Реальный)
n	Показатель упрочнения.(Реальный)
\(\epsilon_{p}^{max}\)	Пластическая деформация отказа. По умолчанию = 1030 (Реал)
\(\sigma_{max0}\)	Максимальное напряжение. По умолчанию = 1030 (Реал)	\([Pa]\)
\(\dot{\epsilon}_{0}\)	Минимальная скорость деформации. По умолчанию = 1,0. (Реал)	\([\frac{1}{s}]\)
m	Показатель скорости деформации. По умолчанию = 0,0. (Реал)
r00	Параметр Ланкфорда 0 градусов. 5 По умолчанию = 1,0 (реальное)
r45	Параметр Ланкфорда 45 градусов. По умолчанию = 1,0. (Реал)
r90	Параметр Ланкфорда 90 градусов. По умолчанию = 1,0. (Реал)
Доходность0	Флаг стресса доходности. = 0 Средний входной предел текучести. = 1 Предел текучести в ортотропном направлении 1. (Целое число)

Пример (Сталь)

#RADIOSS STARTER

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/UNIT/1

unit for mat

                 kg                  mm                  ms

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#-  2. MATERIALS:

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/MAT/HILL/1/1

void_steel

#              RHO_I

              7.8E-6

#                  E                  NU

                 210                  .3

#                  A           EPSILON_0                   n             EPS_max          SIGMA_max0

                 .17                  .2                 .45                   0                   0

#          EPS_DOT_0                   m

                   0                   0

#                r00                 r45                 r90                       Iyield0

                 .75                   1                1.25                             0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#ENDDATA

/END

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Комментарии

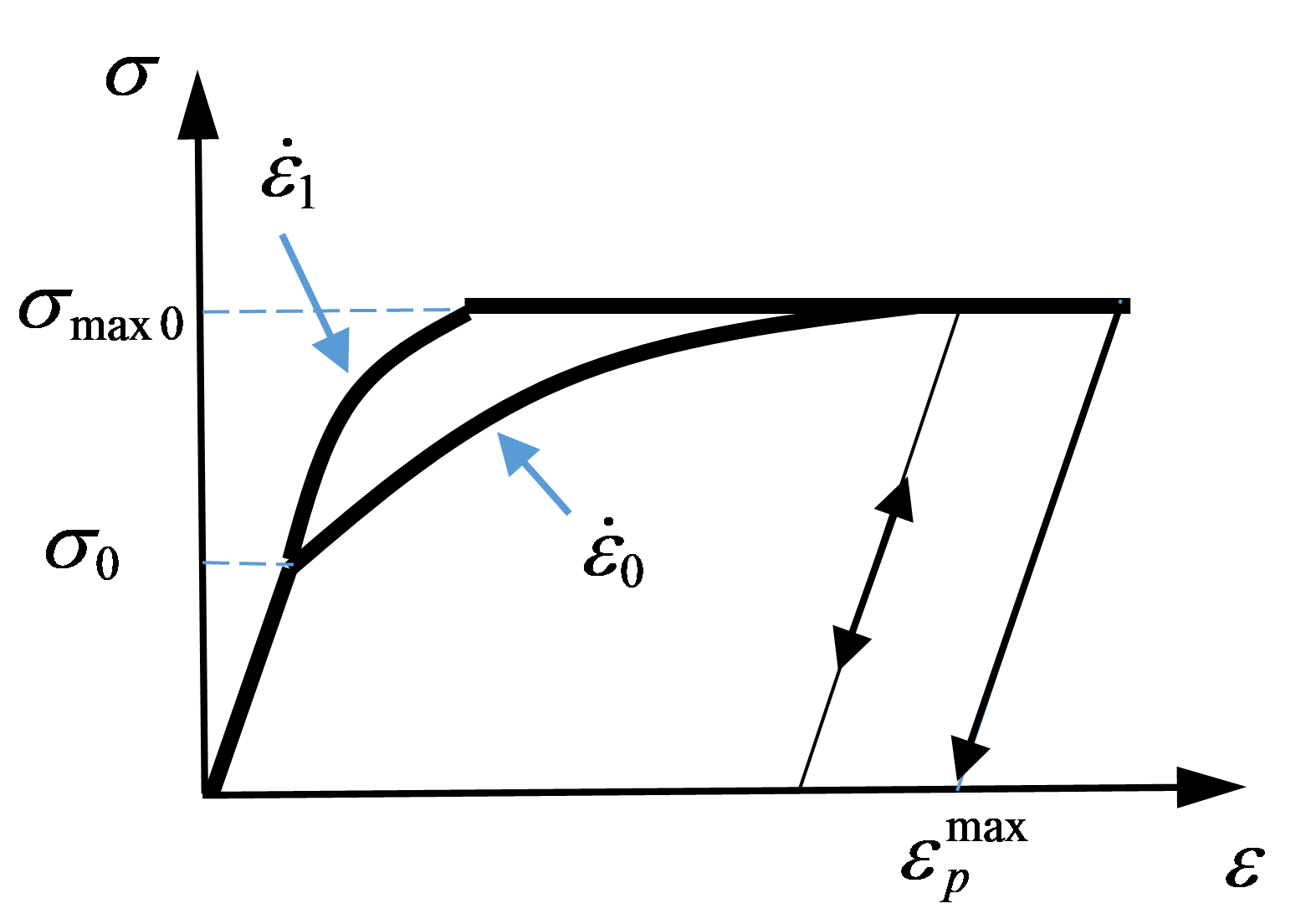
Предел текучести определяется

как:

\(\sigma_{y}=a(\epsilon_{0}+\epsilon_{p})^{n}max(\dot{\epsilon},\dot{\epsilon}_{0})^{m}\) Предел упругости задан

автор:
\(\sigma_{0}=a(\epsilon_{0})^{n}(\dot{\epsilon}_{0})^{m}\) Где, \(\epsilon_{p}\) Пластическая деформация \(\dot{\epsilon}\) Скорость деформации

Предел текучести сравнивается с

эквивалентное напряжение:

\(\sigma_{eq}=\sqrt{A_{1}\sigma_{1}^{2}+A_{2}\sigma_{2}^{2}−A_{3}\sigma_{1}\sigma_{2}+A_{12}\sigma_{12}^{2}}\) .. image:: images/mat_law32_hill_starter_r_mat_law32_yield_stress.png

alt

mat_law32_yield_stress

(Рисунок 1.)

Этот материальный закон следует использовать с

тип набора свойств /PROP/TYPE10 (SH_COMP) или /PROP/TYPE9 (SH_ORTH).

Итеративное проектирование (Iplas

=1) и радиальный возврат (Iplas =2) для напряжения в плоскости оболочки пластик имеется.

Углы для параметров Ланкфорда равны

определяется относительно ортотропного направления 1.

\(R=\frac{r_{00}+2r_{45}+r_{90}}{4}H=\frac{R}{1+R}A_{1}=H(1+\frac{1}{r_{00}})A_{2}=H(1+\frac{1}{r_{90}})A_{3}=2HA_{12}=2H(r_{45}+0.5)(\frac{1}{r_{00}}+\frac{1}{r_{90}})r_{00}=\frac{A_{3}}{2A_{1}−A_{3}}r_{45}=\frac{1}{2}(\frac{A_{12}}{A_{1}+A_{2}−A_{3}}−1)r_{90}=\frac{A_{3}}{2A_{2}−A_{3}}\) Параметры Ланкфорда

\(r_{\alpha}\) это соотношение пластическая деформация в плоскости и пластическая деформация в направление толщины \(\epsilon_{33}\)

.

\(r_{\alpha}=\frac{d\epsilon_{\alpha+\pi/2}}{d\epsilon_{33}}\) Где, \(\alpha\)

есть угол к ортотропному направлению 1.

Это параметры Ланкфорда

\(r_{\alpha}\) может быть определен из простого испытания на растяжение под углом \(\alpha\)

.: Более высокое значение R

означает лучшую формуемость.

Если были получены пределы текучести

в ортотропном направлении 1 определим Доходность0 =1; иначе Доходность0 =0.

Когда

\(\epsilon_{p}\) достигает значения \(\epsilon_{p}^{max}\) , в одной точке интеграции,

тогда соответствующий элемент оболочки

удален.